Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 70

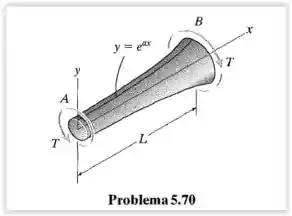
O contorno da superfície do eixo é definido pela equação y = e a x , onde a é uma constante. Se o eixo for submetido a um torque T em suas extremidades, determine o ângulo de torção na extremidade A em relação à extremidade B. O módulo de cisalhamento é G.

Passo 1

Oi galera! Tudo bem com vocês?

O problema nos informa que o contorno da superfície do eixo é dado pela equação y = e a x .

Podemos encontrar o ângulo de torção ϕ A / B através da expressão:

ϕ = ∫ 0 L T d x J G

Devemos lembrar que o raio é a medida do centro até qualquer ponto da circunferência, portanto a variação dele equivale a nossa equação do contorno da superfície. Substituindo, temos:

ϕ A B = ∫ 0 L T d x π 2 ⋅ e a x 4 ⋅ G

Resolvendo a integral:

ϕ A / B = 2 T G π ∫ 0 L 1 e a x 4 d x

Aplicando a integração por substituição ( u = a x ):

ϕ A / B = 2 T G π ∫ 0 a L 1 a e 4 u d u

Retirando a constante:

ϕ A / B = 2 T G π a ∫ 0 a L 1 e 4 u d u

ϕ A / B = 2 T G π a ∫ 0 a L e - 4 u d u

Aplicando a integração por substituição ( v = - 4 u ):

ϕ A / B = 2 T G π a ∫ 0 - 4 a L - 1 4 e v d v

Retirando a constante:

ϕ A / B = 2 T G π a - 1 4 ∫ 0 - 4 a L e v d v

ϕ A / B = 2 T G π a - 1 4 e v 0 - 4 a L  

Simplificando:

ϕ A / B = - T 2 π a G e v 0 - 4 a L  

ϕ A / B = T 2 a π G ⋅ ( 1 - e - 4 a L )

Resposta

ϕ A / B = T 2 a π G ⋅ ( 1 - e - 4 a L )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois eixos de aço sólidos são ajustados com flanges que em seguida são conectadas por parafusos como mostrado. Os parafusos são ligeiramente subdimencionados de modo que permitam uma rotação relativa
Para o eixo de seção circular do Problema 3.98, determine (a) a intensidade do torque T necessário para que eixo sofra um giro de 15 ° e (b) o raio do correspondente núcleo elástico.
A barra circular de seção cheia AB é feita de aço elastiplástico com T E = 151,7M P aeG = 77,2G P a . Sabendo que um torque T = 8473k N * m m é aplicado à barra e depois removido, determine a tensão d
Um eixo sólido de seção circular com 18m m de diâmetro é feito de um material considerado elastoplástico com t y =145M P a e G = 77,2G P a . Para um eixo com 1,2 m de comprimento, determine a máxima t
Uma barra circular cheia é feita de um material considerado elastoplástico chamado de T E e ϕ E ⋅ respectivamente,o torque se o ângulo de torção no início do escoamento, determine o ângulo de torção f