Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 73
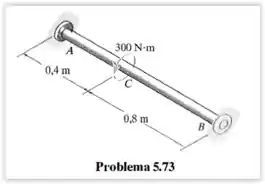
O eixo de aço A-36 tem diâmetro de e está preso nas extremidades e . Se for submetido ao momento, determine a tensão de cisalhamento máxima nas regiões e do eixo.
Passo 1
Oi, gente! Tudo joia?
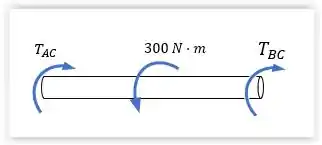
Para resolver esse problema vamos primeiro fazer o diagrama de corpo livre.
Fazendo o somatório dos momentos de inércia, temos que:
É uma viga engastada nas duas extremidades, tem sentido oposto à Então:
Como o diâmetro e o material é o mesmo em todo o eixo, podemos cortar e :
Portanto, já podemos saber quem é e :
Passo 2
Para encontramos a tensão de cisalhamento máxima, usamos:
Em que é o raio e o momento polar de inércia, , é dado por:
Para o segmento ,
Para o segmento ,
Resposta
Exercícios de Livros Relacionados
Duas hastes solidas de latão AB e CD são brasadas junto a uma luva EF. Determine a razão d 2 / d 1 para qual ocorre a máxima tensão de cisalhamento nas hastes e na luva.
sabendo que a tensão de cisalhamento admissível é de 8 ksi para o eixo escalonado mostrado, determine a intensidade T do maior torque que pode ser transmitido pelo eixo quando o raio do adoçamento é (
O eixo sólido mostrado é feito de aço doce considerado elastoplástico com T E = 145M P a . Determine o raio do núcleo elástico causado pela aplicação de um torque igual a 1,1T E em que T E é a intensi
Observa-se que um clipe de papel pode ser girado por várias voltas com a aplicação de um torque de proximidade 60 m N ⋅ m . Sabendo que o diâmetro do fio utilizado no clipe é de 0,9 m m , determine o
O eixo composto mostrado consiste em uma jaqueta de latão de 5.08 mm de espessura ( G l a t ã o = 39G P a ) ã unido a um núcleo de aço de 40 mm de diâmetro G a ç o = 77.2G P a ç . Sabendo que o eixo e