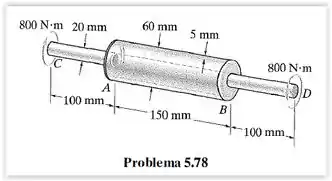
O eixo composto tem uma seção média que indica o eixo maciço de de diâmetro e um tubo soldado a flanges rígidas em e . Despreze a espessura das flanges e determine o ângulo de torção da extremidade do eixo em relação à extremidade . O eixo é submetido a um torque de . O material é aço A-36.

O problema nos fornece como dados:

Aço A-36, portanto

Vamos então construir o diagrama de corpo livre:

Fazendo o somatório dos momentos, temos:

Analisando a figura e a disposição dos torques, vemos que na seção :

Em que, momento polar de inércia, , para o eixo é dado por:

E para o tubo:

Substituindo e simplificando:

Antes de substituis os valores, vamos observar que na figura ele mostra que a espessura do tubo é . Tendo em vista que o seu raio externo é , então o raio interno será:

Podemos cortar os termos que são iguais em ambos os membros, como o comprimento , o e o (eixo e tubo de mesmo material). Calculando, chegamos à: