Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 65

Uma barra circular delgada é sustentada em um plano vertical por um suporte em A. Uma mola de constante k = 45 N/m e comprimento indeformado igual ao arco de círculo AB está presa ao suporte e enrolada frouxamente em volta da barra. Um colar C de 220 g, não ligado à mola, pode deslizar sem atrito ao longo da barra. Sabendo que o colar é liberado do repouso a um ângulo θ em relação à vertical, determine (a) o menor valor de θ para que o colar passe por D e atinja o ponto A, (b) a velocidade do colar quando ele atingir o ponto A.

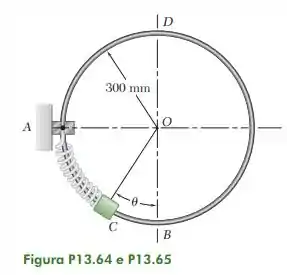
Fonte: Beer – Dinâmica – 9ª ed

Passo 1

Olá pessoal, tudo bem?

Bora lá!!

Bem, vamos analisar o problema de uma forma bem parecida com o problema 13.64.

Primeiro devemos nos atentar aos momentos descritos nesse problema. Então, temos os pontos A, B, C e D dados no enunciado.

E vamos lembrar novamente que a conservação da energia:

E C 1 + E P 1 + E E 1 = E C 2 + E P 2 + E E 2         ( 1 )

Passo 2

Agora vamos as nossas considerações:

  1. As condições do ponto C são as mesmas do problema 13.64, com a diferença que agora queremos encontrar o ângulo θ .
  2. Podemos comparar o instante em C com o instante em D.

Mas porquê? Por que o ponto D é o mais alto da barra, e sabemos que quando o colar atinge o ponto mais alto, sua velocidade naquele instante é nula. Ou seja, em D, só teremos energia potencial. Vejamos o esboço:

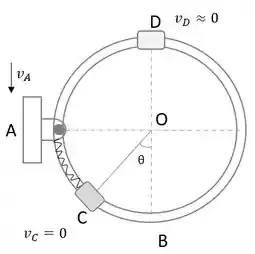
Passo 3

Agora é só alegria! A partir dessas análises, vamos para a conservação da energia.

Desmembrando a eq. 1, temos:

0 + m g R 1 - c o s θ + 0 = 0 + 0 + m g H

Substituindo os valores:

0,22 * 9,81 * 0,3 1 - c o s θ + 1 2 45 * 0,3 * θ 2 = 0 + 0 + 0,22 * 9,81 * 2 * 0,3

Isolando θ , encontramos que:

2,25 θ 2 - 0,647 c o s θ = 0,647  

Assim, resolvendo a equação:

θ = 0,3724   r a d       →         θ = 42,7 0

Passo 4

Agora vamos encontrar qual a velocidade adquirida pelo colar no ponto A (que possui energia potencial e cinética):

Então podemos aplicar a conservação da energia comparando o ponto A com algum outro. Escolhamos o ponto D:

0,22 v A 2 2 + 0,22 * 9,81 * 0,3 = 0,22 * 9,81 * 2 * 0,3                 →         0,11 v A 2 = 0,64746

Assim, resolvendo a equação, encontramos:

v m a x = 2,43 m s

Resposta

Portanto:

Letra a) θ = 42,7 0

Letra b) v m a x = 2,43 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bola de 0,5 kg é disparada pelo dispositivo com mola mostrado. Determine a menor rigidez k necessária para disparar a bola e uma distância máxima s=750 mm plano acima após a mola ser empurrada para
No instante mostrado, o ponto P no cabo tem uma velocidade de v P = 12m / s , que está aumentando a uma taxa de a P = 6m / s 2 . Determine a potência de entrada do motor M neste instante se ele opera
Se a superfície de contato entre o bloco de 20 kg e o solo é lisa, determine a potência de força F quando t = 4 s. Inicialmente, o bloco está em repouso.
Se F = 10 sN , onde s é dado em metros e a superfície de contato entre o bloco e o solo é lisa, determine a potência de força F quando s = 5 m. Inicialmente, o bloco de 20 kg está em repouso.
Se a carga de 50 kg A é içada pelo motor M de maneira que a carga tenha uma velocidade constante de 1,5 m/s, determine a potência de entrada do motor, o qual opera com uma eficiência de ϵ = 0,8 .