Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 20

Para a barra composta do Prob 2.10, determinar a maior carga P admissível se em valores absolutos a deformação total da barra e sua máxima tensão normal não podem exceder a 0,2 m m e 75 M P a , respectivamente

Passo 1

Vamos começar calculando a reação de apoio e as forças internas na estrutura:

+ ↑ ∑ F y = 0 ⇒ - P - 40   k N + R = 0

R = P + 40   k N

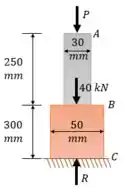
Agora vamos fazer uma seção sobre o porto B. Vamos estudar os esforços internos na barra:

Passo 2

Vamos calcular também as áreas de seção transversal de cada segmento.

A A B = π d A B 2 4 = π ⋅ 30   m m 2 4 = 225 π   m m 2

A B C = π d B C 2 4 = π 50   m m 2 4 = 625 π   m m 2

Passo 3

A forma de resolver esse tipo de questão é testando! Primeiro vamos calcular a maior carga permitida pela deformação. E depois vamos testar a maior carga permitida pela tensão. A resposta será o MENOR valor calculado.

Vamos testar então utilizando a deformação. A Equação 2.8 do livro é a que devemos utilizar nesse caso:

δ = ∑ P L A E

δ = P A B L A B A A B E A B + P B C L B C A B C E B C

Aplicamos os valores:

0,2   m m = P ⋅ 250   m m 225 π   m m 2 ⋅ 200   G P a + P + 40 k N ⋅ 300   m m 625 π   m m 2 ⋅ 105   G P a

Colocamos todas as unidades no S.I. assim, não vamos mais precisar nos preocupar com elas.

0,2 ⋅ 10 - 3 m = P ⋅ 250 ⋅ 10 - 3 m 225 π ⋅ 10 - 6 m 2 ⋅ 200 ⋅ 10 9 P a + P + 40 ⋅ 10 3 N ⋅ 3 00 ⋅ 10 - 3 m 625 π ⋅ 10 6 m 2 ⋅ 105 ⋅ 10 9 P a

Vamos efetuar as divisões:

0,2 ⋅ 10 - 3 = 1,768 ⋅ 10 - 9 ⋅ P + 1,455 ⋅ 10 - 9 ⋅ P + 5,821 ⋅ 10 - 5

Isolamos o P :

3,223 ⋅ 10 - 9 ⋅ P = 1,4179 ⋅ 10 - 4

Como todas as unidades estão no S.I. a unidade do P será newtons:

P = 43993,17   N

P = 4 4   k N

Passo 4

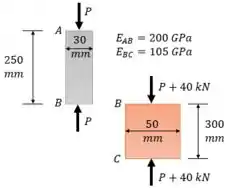
Agora vamos considerar a tensão máxima sobre a barra. Primeiro, vamos imaginar que a tensão máxima ocorre na seção AB:

σ m á x = P A B A A B

75 M P a = P 225 π   m m 2

P = 75   M P a ⋅ 2 25 π   m m 2

P = 53014,38   N

P = 53 , 01   k N

Agora vamos imaginar que a tensão máxima ocorra na seção BC:

σ m á x = P B C A B C

75   M P a = P + 40 k N 625 π   m m 2

P = - 40   k N + 75 M P a ⋅ 625 π   m m 2

P = 107262,16   N

P = 107,26   k N

Passo 5

Calculamos 3 possibilidades para o valor de P . Porém devemos escolher o menor valor:

P = 44   k N

Resposta

P = 44   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de poliestireno consiste de duas porções cilíndricas AB e BC, restringidas em ambas as extremidades, e suporta duas cargas de 27 k N , como indicado. Sabendo-se que E = 3,1 G P a , determina
Para a barra composta do Prob. 2.9, determinar ( a ) a carga, para a qual a deformação total da barra resulta nula; ( b ) a correspondente deflexão no ponto B .
Uma carga vertical P é aplicada em A, na seção superior de um tronco de cone de altura h , raio mínimo a e raio máximo b . (a) Determine a deflexão no ponto A, se E for o módulo de elasticidade.
Duas barras cilíndricas maciças são ligadas em B e carregadas como mostrado. A barra A B é de aço ( E = 200G P a ) e a barra B C é de latão ( E = 105G P a ) . Determinar: ( a ) a deformação total da b
Duas barras cilíndricas maciças são ligadas em B e carregadas como mostrado. A barra A B é de aço ( E = 200G P a ) e a barra B C é de latão ( E = 105G P a ) . Determinar: ( a ) a deformação total da b