Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 56

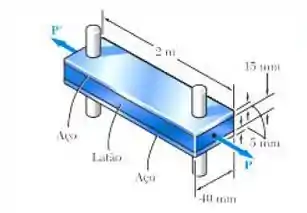
Determine a força P máxima que pode ser aplicada à barra de latão do Problema 2.55 se a tensão admissível nas barras de aço for de 30 MPa e a tensão admissível na barra de latão, 25 MPa.

Passo 1

Fala aí galerinha tudo belezinha? O exercício pede para que a gente determine a força P, para isso vamos resgatar os valores de tensões do Problema 2.55 para obter as tensões de fabricação.

σ a * = 22,028   M P a σ b * = 14,6853   M P a

Tensões admissíveis: σ s ,   a l l = 30   M P a ,     σ b ,   a l l = 25   M P a  

Para determinar o aumento da tensão tem-se.

σ a = 30 - 22,028 = 7,9720   M P a σ b = 25 + 14,6853 = 39,685   M P a

E as deformações respectivas de cada material é determinado a seguir:

ε s = σ s E s = 7,9720   x   10 6 200   x   10 9 = 39,860   x   10 - 6 ε b = σ b E b = 39,685   x   10 6 105   x   10 9 = 377,95   x   10 - 6

Um valor menor governa ∴ ε = 39,860     x   10 - 6

Passo 2

Calculando a área do elemento temos:

Áreas: A a = 2   x   5   x   40 = 400 m m 2 = 400   x   10 - 6 m 2 A b = 15   x   40 = 600 m m 2 = 600   x   10 - 6 m 2

As forças são determinadas a seguir:

P a = E a A ε = 200   x   10 9   x   400   x   10 - 6   x   39,860   x   10 - 6 = 3,1888   x   10 3 N P b = E b A b ε = 105   x   10 9   x   600   x   10 - 6   x   39,860   x   10 - 6 = 2,5112   x   10 - 3 N

Força adicional total admissível:

P = P s + P b = 3,1888   x   10 3 + 2,5112   x   10 - 3 N

Resposta

P = 5,70   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra de seção vazada de parede fina A B tem uma seção transversal não circular com espessura de parede não uniforme. Usando a expressão dada na equação 3.5 da seção 3.1 e a expressão para a desnida
Cada barra de treliça mostrada na figura é feita de aço e têm seção transversal uniforme com área de 5i n 2 . Usando E = 29 × 10 6G P a , determine o deslocamento vertical do nó B provocado pela aplic
Cada elemento da treliça mostrada é feito de aço. A área da seção transversal do elemento B C é de 800m m 2 , e para todos os outros elementos a área é de 400m m 2 . Utilizando E = 200G P a , determin
Na treliça mostrada, todos os elementos são feitos do mesmo material e têm a área da seção trasnversal indicada. Determine a energia de deformação da treliça quando lhe é aplicada a força P .
Usando E = 73,1G P a , determine de forma aproximada a máxima energia de deformação que a barra de alumínio acumulará se a tensão normal admissóivel é σ a d m = 151,7M P a .