Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 171

A barra A B de comprimento R = 300   m m gira em torno A com velocidade angular constante ω 1 de 5   r a d / s no sentido horário. Ao mesmo tempo, a barra B D de comprimento r = 160   m m gira em torno de B com velocidade angular constante ω 2 = 3   r a d / s no sentido anti- -horário com relação da barra A B . Sabendo que 60 ° , determine para a posição mostrada na figura, a aceleração do ponto D .

Passo 1

Bora pra questão 171 agora, meus caros (as)!

Bom! Temos que mostrar aqui que a aceleração do ponto D passa por meio do ponto A .

Pois muito bem! Antes de qualquer coisa, vamos a algumas convenções...

Primeiro o sentido de rotação... Normalmente costumamos chamar o sentido horário de negativo e o sentido anti-horário de positivo. E como no sentido de rotação, a gente geralmente usa o versor k ^ , então...

ω → 1 = - ω 1 k ^ = ( - 5   r a d / s )   k ^

ω → 2 = ω 2 k ^ = ( 3   r a d / s )   k ^

Agora, vamos dar uma olhada na barra A B ! Essa barra só executa rotação... Logo;

Ω → = ω → 1 = - ω 1 k ^

Continuando nosso raciocínio, bora fazer um esboço do nosso sistema destacando os vetores posição de nosso interesse...

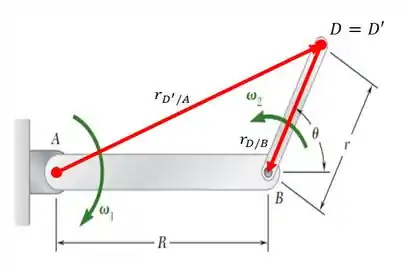
Onde D ' é o ponto do plano de rotação da barra B D , que chamaremos de F !

E esse ponto coincide exatamente com o ponto D . Baseado na geometria, temos então, que...

r → D ' / A = r → D / A = R + r cos ⁡ θ i ^ + ( r sen ⁡ θ ) j ^

r → D / B = r cos ⁡ θ i ^ + ( r sen ⁡ θ ) j ^

Passo 2

Pronto! As informações mais importantes, já temos em mãos!

Se liga! A velocidade de D em relação ao plano de rotação, é dada por...

v → D / F = ω → 2 × r → D / B

v → D / F = ω 2 k ^ × [ r cos ⁡ θ i ^ + ( r sen ⁡ θ ) j ^ ]

v → D / F = ω 2 r ( - sen �� θ i ^ + cos ⁡ θ j ^ )

Presta atenção, agora! A aceleração no ponto D , como em geral nas questões desse capítulo, vem na seguinte forma...

a → D = a → D ' + a → D / F   + 2 Ω → × v → D / F  

Passo 3

Por isso, a nossa missão agora, é ir atrás desses três itens; a → D ' , a → D / F   e 2 Ω → × v → D / F   !

Primeiro, vamos obter 2 Ω → × v → D / F   :

2 Ω → × v → D / F   = 2 ω 1 k ^ × [ ω 2 r ( - sen ⁡ θ i ^ + cos ⁡ θ j ^ ) ]

2 Ω → × v → D / F   = - 2 ω 1 ω 2 r ( cos ⁡ θ i ^ + sen ⁡ θ j ^ )

Já a aceleração a → D ' é dada por...

a → D ' = - Ω 2 r D / A

a → D ' = - ω 1 2 r D / A

a → D ' = - ω 1 2 [ R + r cos ⁡ θ i ^ + ( r sen ⁡ θ ) j ^ ]

E por fim, falta obter a aceleração do ponto D em relação ao plano de rotação, é igual à...

a → D / F   = - ω 2 2 r → D / B

a → D / F   = - ω 2 2 [ r cos ⁡ θ i ^ + ( r sen ⁡ θ ) j ^ ]

a → D / F   = - ω 2 2 r [ cos ⁡ θ i ^ + ( sen ⁡ θ ) j ^ ]

Substituindo assim, os valores de cada variável, obtemos que...

a → D = a → D ' + a → D / F   + 2 Ω → × v → D / F  

a → D = - ω 1 2 [ R + r cos ⁡ θ i ^ + ( r sen ⁡ θ ) j ^ ] - ω 2 2 r [ cos ⁡ θ i ^ + ( sen ⁡ θ ) j ^ ] - 2 ω 1 ω 2 r ( cos ⁡ θ i ^ + sen ⁡ θ j ^ )

a → D = - ω 1 2 R i ^ - ω 1 2 + 2 ω 1 ω 2 + ω 2 2 2 ( r cos ⁡ θ i ^ + r sen ⁡ θ j ^ )

a → D = - [ ω 1 2 R i ^ + ω 1 + ω 2 2 r cos ⁡ θ i ^ + r sen ⁡ θ j ^ ]

Sabendo então os valores de ω 1 , ω 2 , r , R e θ :

a → D = - [ ω 1 2 R i ^ + ω 1 + ω 2 2 r cos ⁡ θ i ^ + r sen ⁡ θ j ^ ]

a → D = - [ ( - 5 ) 2 ⋅ 300 i ^ + - 5 + 3 2 160 cos ⁡ 60 ° i ^ + 160 sen ⁡ 60 ° j ^ ]

a → D = - ( 7820   m m / s 2 ) i ^ - ( 554,256   m m / s 2 ) j ^

a → D = - ( 7 , 82   m / s 2 ) i ^ - ( 0,55   m / s 2 ) j ^

Escrevendo em módulo e ângulo de direção...

a D = - 7,82   m / s 2 2 + - 0,55   m / s 2 2 ∠ tan - 1 ⁡ - 0,55   m / s 2 - 7,82   m m / s 2

a D = 7,84   m / s 2   ⦫ 4,05 °

Resposta

a D = 7,84   m / s 2   ⦫ 4,05 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco mostrado tem uma velocidade angular constante de 500 rpm no sentido anti-horário. Sabendo que a haste BD tem 250 mm de comprimento, determine a aceleração do colar .D quando (a) θ = 90 ∘ , ( b
No compressor de ar de dois cilindros mostrado, as bielas BD e BE têm cada uma 190 mm de comprimento e a manivela AB gira em torno do Ponto fixo A com uma velocidade angular constante de 1500 rpm no s
O braço AB tem uma velocidade angular constante de 16 rad / s no sentido anti-horário. No instante em que θ = 0 , determine a aceleração (a) do colar D, (b) do ponto médio G da barra BD.
Sabendo que a manivela AB gira em torno do Ponto A com uma velocidade angular constante de 900 rpm no sentido horário, determine a aceleração do pistão P quando θ = 60 ∘ .
Sabendo que a manivela AB gira em torno do Ponto A com uma velocidade angular constante de 900 rpm no sentido horário, determine a aceleração do pistão P quando 0 = 120 °.