Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 209

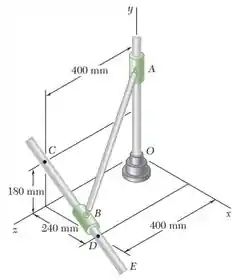
A barra AB de comprimento de 500 mm está conectada por juntasrotuladas aos colares A e B, que deslizam ao longo das duas barrasmostradas na figura. Sabendo que o colar B aproxima-se do ponto Ea uma velocidade constante de 400 mm/s, determine a velocidade docolar A quando o colar B passa pelo ponto C.

Passo 1

E ai gurizada tudo belezinha???

Geometria: l A B 2 = x A / B 2 + y A / B 2 + z A / B 2 :                     25 ² = 0 + y A / B 2 + ( - 20 ) ²

y A / B = 12   i n .

r A / B = 6   i n . j - 8   i n . k

r D / C = 12   i n . i + 9   i n . j

l C D = 12 2 + ( - 9 ) ² = 15   i n .

Velocidade no colar B: v B = v B r A / C l C D

v B = ( 20 ) ( 12   i - 9   j ) 15 = ( 16   i n . / s ) i - ( 12   i n . / s )   j

Velocidade do colar A: v A = v A   j

v A = v B + v A / B

Passo 2

Onde v A / B = ω A / B + r A / B

Observando que v A / B é perpendicular a r A / B , obtemos r B / A ∙ v B / A = 0    

Formando r A / B ∙ v A , nos temos r A / B ∙ v A = r A / B ∙ ( v B + v A / B )

= r A / B ∙ v B + r A / B ∙ v A / B ou r A B ∙ v A = r A / B ∙ v B

Da equação: 6 j - 8 k ) ∙ ( v A   j ) = ( 8 j - 8 k ) ∙ ( 16 i - 12 j )   6 v A

= ( 6 ) ( - 12 )

v A = - 12   i n . / s  

Resposta

v A = - ( 12   i n . / s ) j  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante considerado, a antena de radar mostrada na figura gira em torno da origem das coordenadas com uma velocidade angular ω = ω x i ^ + ω y j ^ + ω z k ^ . Sabendo que v A y =300m m / s , v B y
No instante considerado, a antena de radar mostrada na figura gira em torno da origem das coordenadas com uma velocidade angular ω = ω x i ^ + ω y j ^ + ω z k ^ . Sabendo que v A x =10 0m m / s , v A
O conjunto de pás de um ventilador oscilante gira com uma velocidade angular constante ω 1 = - 360r p m i ^ em relação à caixa do motor. Determine a aceleração angular do conjunto de pás, sabendo que,
Um rotor de um motor elétrico gira a uma taxa constante ω 1 = 1 800r p m . Determine a aceleração angular do rotor quando o motor é girado sobre o eixo y com a velocidade constante ω 2 de 6r p m no se
No sistema mostrado na figura, o disco A é livre para girar sobre a barra horizontal AO. Considerando que o disco B é estacionário ( ω 2 =0 ) e que o eixo OC gira com velocidade angular constante ω 1