Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 122
A barra curva tem uma massa por unidade de comprimento. Determine o momento do peso da barra em relação ao ponto .
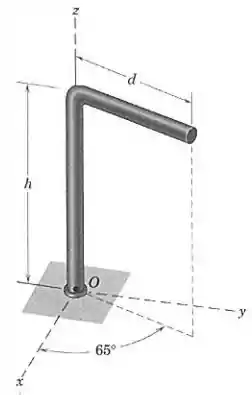
Passo 1
Note que a força que causa momento em torno de é somente aquela equivalente ao peso da parte da barra de comprimento , conforme mostra a figura a seguir, em vermelho:
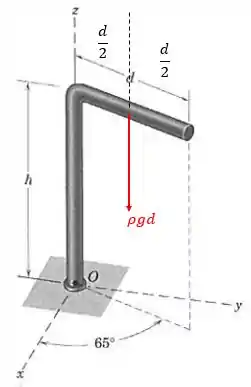
A massa dessa parte da barra é (densidade vezes comprimento), e portanto seu peso é , que atua no seu centro de gravidade, ou seja, em seu ponto médio.
Passo 2
Então, temos:
Analogamente,
A força peso não produz momento em relação ao eixo :
Logo,
Resposta
Exercícios de Livros Relacionados
As direções de rotação dos eixos de entrada A e de saída B no redutor de engrenagens estão indicadas pelas setas curvas tracejadas. Um torque de entrada (binário) de 80N ∙ m é aplicado ao eixo A na di
Determine o momento da força F em relação ao ponto O . Expresse o resultado como um vetor cartesiano.
Determine o momento produzido por F 1 em relação ao ponto O . Expresse o resultado como um vetor cartesiano.
38. Determine o momento produzido por F 2 em relação ao ponto O. Expresse o resultado como um vetor cartesiano.
44. Uma força F → = 6 i - 2 j + 1 kk N produz um momento M 0 = 4 i + 5 j - 14 kk N ⋅ m em relação a origem das coordenadas, o ponto O. Se a força age em um ponto tendo uma coordenada x de x = 1m , det