Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 100
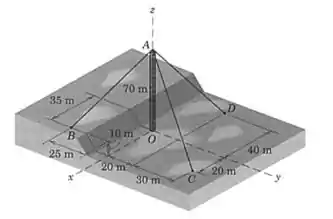
A torre de transmissão de microondas com de altura é equilibrada por três cabos de amarração, como mostrado. O cabo suporta uma força trativa de . Expresse em forma vetorial a força correspondente no ponto .
Passo 1
O primeiro passo é encontrar o vetor unitário na direção do cabo . Para isso vamos usar as dimensões que estão na figura do enunciado:
Lembrando que é um vetor que passa exatamente por cima do cabo :
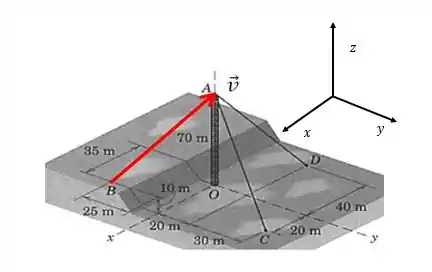
E agora podemos calcular o módulo desse vetor:
E então o vetor unitário é:
Passo 2
E agora o vetor da tração é simplesmente o módulo multiplicado pelo vetor unitário
Resolvido!
Resposta
A força correspondente no ponto é .
Exercícios de Livros Relacionados
Determine o ângulo θ entre a força de 200N e a linha O C .
Se M está no centro da face A B C D do sólido retangular, expresse F como um vetor em termos dos vetores unitários i , j e k . Determine a projeção escalar de F ao longo da linha A E . Os valores de F
Uma força F é aplicada à superfície da esfera como mostrado. Os ângulos θ e ϕ localizam o ponto P e M é o ponto médio de O N . Expresse F em forma vetorial, usando as coordenadas x , y e z dadas.
A porta de acesso é mantida na posição aberta a 30 ° por uma corrente A B . Se a força trativa na corrente é de 100N , determine a projeção desta força sobre o eixo diagonal C D da porta.
A placa retangular é suportada por dobradiças ao longo de seu lado B C e pelo cabo A E . Se a força trativa no cabo vale 300N , determine a projeção sobre a linha B C da força exercida pelo cabo sobre