Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 109
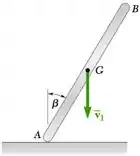
A barra delgada AB, de comprimento L, forma um ângulo com o eixo vertical quando bate na superfície sem atrito mostrada na figura com uma velocidade vertical e sem velocidade angular. Admitindo que o impacto seja perfeitamente elástico, deduza uma expressão para a velocidade angular da barra imediatamente após o impacto.
Passo 1
O enunciado pede que a gente deduza uma expressão para a velocidade angular da barra imediatamente após o impacto.
Momento de inércia.
Impacto perfeitamente elástico.
Cinética.
Passo 2
Componentes horizontais:
Cinemática.
Componentes de velocidade :
Momentos sobre A:
Resposta
Exercícios de Livros Relacionados
No Problema, determine o valor necessário da constante decada mola se a amplitude da vibração em regime permanente deveser de 0,4 mm.
Escreva as equações diferenciais definindo (a) os deslocamentos da massa me do Ponto A, (b) as cargas nos capacitores do análogo elétrico
Dois blocos A e B, cada um com massa m, são apoiados como mostrado por três molas da mesma constante k. Os blocos A e B são conectados por um painel de instrumentos e o bloco B é conectado ao solo por
O bloco mostrado na figura é abaixado em 30 mm da sua posiçãode equilíbrio e então liberado. Sabendo que depois de 10 ciclos odeslocamento máximo do bloco é de 12,5 mm, determine (a) o fatorde amortec
A suspensão de um automóvel pode ser aproximada pelo sistema simplificado de mola e painel mostrado. (a) Escreva a equação diferencial que define o deslocamento vertical da massa m quando o sistema se