Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 94

No Problema 17.81, determine a velocidade do tubo em relação à barra quando o tubo bate na extremidade E do conjunto.

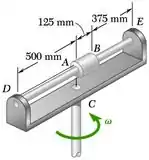
PROBLEMA 17.81 Um tubo AB de 1,6 kg desliza livremente na barra DE que pode girar livremente no plano horizontal. Inicialmente o conjunto está rodando com velocidade angular ω = 5 rad/s e o tubo é mantido na posição por uma corda. O momento de inércia da barra e do braço em torno do eixo vertical de rotação é 0,30 kg ∙ m2 e o momento de inércia centroide do tubo em torno eixo vertical é 0,0025 kg ∙ m2. Se a corda é subitamente rompida, determine (a) a velocidade angular do conjunto após o tubo ter se movido para a extremidade E, (b) a energia perdida pelo impacto plástico em E.

Passo 1

O enunciado pede que a gente determine (a) a velocidade angular do conjunto após o tubo ter se movido para a extremidade E, (b) a energia perdida pelo impacto plástico em E.

Seja o ponto C a intersecção do eixo C com a barra DE. Seja o ponto G o centro de massa do tubo AB.

Massas e momentos de inércia sobre eixos verticais.

m A B = 1.6   kg

I - A B = 0.0025   kg ∙ m 2

I - D C E = 0.30   kg ∙ m 2

Passo 2

Estado 1.

r G / A 1 = 1 2 125 = 62.5   mm

ω 1 = 5   rad/s

v r 1 = 0

Passo 3

Estado 2.

r G / A 2 = 500 - 62.5 = 437.5   mm

ω = ω 2

v r = v r 2 = 0

Passo 4

Momentos sobre C:

I - A B ω 1 + I - D C E ω 1 + m A B v - θ 1 r G / C 1 + 0 = I - A B ω 2 + I - D C E ω 2 + m A B v - θ 2 r G / C 2

I - A B + I - D C E + m A B r G / C 1 2 ω 1 = I - A B + I - D C E + m A B r G / C 2 2 ω 2

0.0025 + 0.30 + 1.6 0.0625 2 5 = 0.0025 + 0.30 + 1.6 0.4375 2 ω 2

0.30875 5 = 0.60875 ω 2

ω 2 = 2.5359   rad/s

Passo 5

Energia cinética.

T = 1 2 I - A B ω 2 + 1 2 I - D C E ω 2 + 1 2 m A B v - 2 = 1 2 I - A B ω 2 + 1 2 I - D C E ω 2 + 1 2 m A B r G / C 2 ω 2 + v - r 2

T 1 = 1 2 0.0025 5 2 + 1 2 1.6 0.0625 2 + 0 = 3.859375   J

T 2 = 1 2 0.0025 2.5359 2 + 1 2 0.30 2.5359 2

+ 1 2 1.6 0.0625 2 2.5359 2 + 1 2 1.6 v - r 2 2 = 1.95737 + 0.8 v - r 2 2

Passo 6

Trabalho. O trabalho das reações do rolamento em C é zero. Como o contato deslizante entre a haste e o tubo é sem atrito, o trabalho da força de contato é zero.

U 1 → 2 = 0

Princípio de trabalho e energia.

T 1 + U 1 → 2 = T 2

3.859375 + 0 = 1.95737 + 0.8 v - r 2 2

Resposta

Velocidade do tubo em relação à haste.

v - r 2 = 1.542   m/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra AB de massa 7,5 kg e comprimento 1 m está presa a um carrinho C de 12,5 kg. Sabendo que o sistema é liberado do repouso na posição mostrada na figura e desprezando o atrito, determine (a) a ve
Uma bala de 45 g é disparada com velocidade de 400 m/s a θ = 5° dentro de um painel quadrado de 9 kg de lado b = 200 mm. Sabendo que h = 150 mm e que o painel está inicialmente em repouso, determine (
No Problema 17.96, determine (a) a distância h requerida para que a reação impulsiva em C seja nula, (b) a velocidade angular correspondente da barra imediatamente após a bala ter se alojado.
Uma bala de 45 g é disparada com velocidade de 400 m/s a θ = 30° dentro de um painel quadrado de 9 kg de lado b = 200 mm. Sabendo-se que h = 150 mm e que o painel está inicialmente em repouso, determi