Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 55

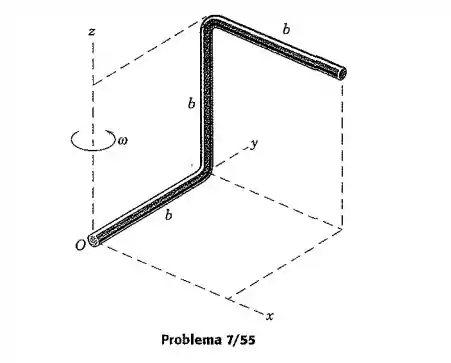
A barra dobrada possui uma massa ρ por unidade de comprimento e gira em relação ao eixo z com uma velocidade angular ω . Determine a quantidade de movimento angular H o da barra em relação à origem fixa O dos eixos, que são presos à barra. Encontre também a energia cinética T da barra.

Passo 1

Para resolvermos esse problema, temos que encontrar as componentes do tensor de inércia da barra girando em torno de cada eixo. Após isso, vamos aplicar na equação de H o para encontrarmos a energia cinética do corpo.

Passo 2

Vamos começar analisando os dados do enunciado. Nos é dito que a barra gira em torno apenas do eixo z , sendo assim ω x = ω y = 0 e isso nos dá que H o será

H o = - I x z ⋅ i - I y z ⋅ j + I z z ⋅ k ⋅ ω

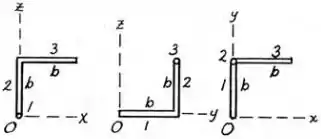
Agora precisamos calcular as componentes do tensor de inércia. Podemos separar todo o sistema em 3 barras como na imagem mostrada acima, assim precisaremos calcular essas componentes para cada barra e somar seus valores.

Para a barra em x - z , teremos que

I x z = ∭ x ⋅ z ⋅ ρ ⋅ d V = 0

I y z = ∭ y ⋅ z ⋅ ρ ⋅ d V = 0

I z z = ∭ x 2 + y 2 ⋅ ρ ⋅ d V = 1 3 ⋅ ρ ⋅ b 3

Em y - z temos

I x z = ∭ x ⋅ z ⋅ ρ ⋅ d V = 0

I y z = ∭ y ⋅ z ⋅ ρ ⋅ d V = 1 2 ⋅ ρ ⋅ b 3

I z z = ∭ x 2 + y 2 ⋅ ρ ⋅ d V = ρ ⋅ b 3

E para x - y vamos ter

I x z = ∭ x ⋅ z ⋅ ρ ⋅ d V = 1 2 ⋅ ρ ⋅ b 3

I y z = ∭ y ⋅ z ⋅ ρ ⋅ d V = ρ ⋅ b 3

I z z = ∭ x 2 + y 2 ⋅ ρ ⋅ d V = 4 3 ⋅ ρ ⋅ b 3

Se somarmos todos os termos, teremos que nosso tensor de inércia tem as componentes

I x z = 1 2 ⋅ ρ ⋅ b 3

I y z = 3 2 ⋅ ρ ⋅ b 3

I z z = 8 3 ⋅ ρ ⋅ b 3

Substituindo agora na equação de H o teremos que

H o = - 1 2 ⋅ ρ ⋅ b 3 ⋅ i - 3 2 ⋅ ρ ⋅ b 3 ⋅ j + 8 3 ⋅ ρ ⋅ b 3 ⋅ k ⋅ ω

H o = ρ ⋅ b 3 ⋅ - 1 2 ⋅ i - 3 2 ⋅ j + 8 3 ⋅ k ⋅ ω

Passo 3

Para encontrarmos a energia cinética do sistema usaremos a seguinte equação

T = 1 2 ⋅ ω ⋅ H O

Substituindo os valores e realizando o produto escalar, encontraremos que:

T = 4 3 ⋅ ρ ⋅ b 3 ⋅ ω 2

Resposta

H o = ρ ⋅ b 3 ⋅ - 1 2 ⋅ i - 3 2 ⋅ j + 8 3 ⋅ k ⋅ ω

T = 4 3 ⋅ ρ ⋅ b 3 ⋅ ω 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A montagem consiste em uma disco de 8 kg e uma barra de 10 kg que está conectada ao disco por um pino. Se o sistema é solto do repouso, determine a aceleração angular do disco. Os coeficientes de atri
A montagem consiste em uma disco de 8 kg e uma barra de 10 kg que está conectada ao disco por um pino. Se o sistema é solto do repouso, determine a aceleração angular do disco, se a barra for removida
O cilindro de 7,5 Kg está inicialmente em repouso sobre uma placa de 2,5 kg. Se um momento de binário M = 60N ∙ m for aplicado ao cilindro, determine a aceleração angular do cilindro e o tempo necessá
Determine o coeficiente de atrito estático mínimo entre o disco e a superfície no Problema 17.114, de maneira que o disco role sem deslizar. Despreze a massa das polias
A roda de 75 kg e um raio de giração K g375m m em relação a seu centro de massa G. Se ela é submetida a um torque M=100N m Determine sua aceleração angular. Os coeficientes de atrito cinético e estáti