Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 92

Determine a frequência natural f n para pequenas oscilações do corpo composto no plano vertical em torno do mancal O . Aproxime o corpo como uma barra esbelta de massa m / 5 e um disco semicircular de massa m , ambos com a dimensão r conforme indicado.

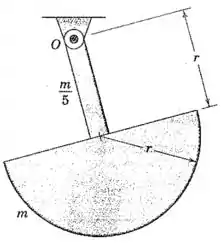
Passo 1

Vamos começar com um diagrama das forças que agem sobre o sistema:

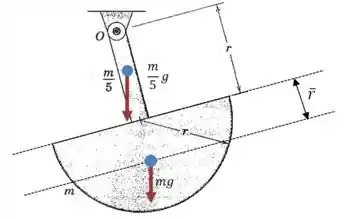
Onde r - é a posição do centro de massa em relação ao centro do disco semicircular:

∑ M O = - m g sen ⁡ θ r + r - -   1 5 m g sen ⁡ θ r 2  

Passo 2

Agora vamos calcular o momento de inércia do sistema em relação ao ponto O :

I O = I b a r r a + I d i s c o

Começando pelo momento de inércia do disco. Aqui precisamos usar o teorema dos eixos paralelos, pois o valor que temos tabelado é o momento em relação ao centro do disco semicircular.

I C = 1 2 m r 2

Então o momento de inércia em relação ao centro de massa do disco é:

I C = I c m + m d 2

I c m = 1 2 m r 2 - m r - 2

E o centro de massa está a uma distância r + r - do ponto O , então:

I d i s c o = I c m + m r + r - 2

I d i s c o = 1 2 m r 2 - m r - 2 + m r + r - 2

Agora vamos olhar para o momento de inércia da barra em relação ao ponto O :

I b a r r a = 1 3   m 5 r 2 = 1 15 m r 2

Então:

I O = 1 15 m r 2 + 1 2 m r 2 - m r - 2 + m r + r - 2

O valor r - = 4 r 3 π pode ser consultao em uma tabela:

I O = 1 15 m r 2 + 1 2 m r 2 - m 4 3 π 2 r 2 + m r 2 1 + 4 3 π 2

Colocando m r 2 em evidência:

I O = m r 2 1 15 + 1 2 - 16 9 π 2 + 16 9 π 2 + 8 3 π + 1

I O = m r 2   1 15 + 3 2 + 8 3 π

Passo 3

Agora vamos substituir tudo isso na equação principal:

∑ M O = I O θ ¨

- m g sen ⁡ θ r + r - -   1 5 m g sen ⁡ θ r 2 = m r 2   1 15 + 3 2 + 8 3 π θ ¨

E podemos aproximar sen ⁡ θ ≅ θ e substituir a expresão r - :

- m g θ r + 4 r 3 π -   1 5 m g θ r 2 = m r 2   1 15 + 3 2 + 8 3 π θ ¨

Agora vamos dividir tudo por m r e isolar θ ¨ :

- g θ 1 + 4 3 π -   1 5 g θ 1 2 = r   1 15 + 3 2 + 8 3 π θ ¨

θ ¨ + 1 + 4 3 π + 1 10 1 15 + 3 2 + 8 3 π g r θ = 0

E podemos resolver essa expressão para obter um único número:

θ ¨ + 0,631 g r θ = 0

Então a frequência f segue a seguinte expressão:

f n = ω n 2 π = 1 2 π 0,631 g r

Resposta

A frequência natural para pequenas oscilações é f n = 1 2 π 0,631 g r .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a amplitude da vibração vertical do reboque com suspensão de molas, enquanto viaja a uma velocidade de 25km/h sobre a estrada ondulada cujo contorno pode ser expresso por um termo de seno ou
Um dispositivo para produzir vibrações é constituído de dois volantes que giram em sentidos opostos, cada um contendo uma massa excêntrica m 0 = 1kg , com um centro de massa a uma distância e = 12mm d
O instrumento sísmico está montado sobre uma estrutura que sofre uma vibração vertical com uma frequência de 5Hz e uma amplitude dupla de 18mm . O elemento sensor possui uma massa m = 2kg , e a rigide
Desenvolva uma expressão para a transmissibilidade T para o sistema da figura. Essa relação é definida como a força máxima transmitida à base dividida pela amplitude F 0 da função de forçamento. Expre
A peça anexa B recebe um movimento horizontal x B = b cos ⁡ ω t . Desenvolva a equação do movimento para a massa m e determine a frequência crítica ω c para a qual as oscilações da massa tornam-se exc