Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 39
A barra esbelta de possui uma massa de e está montada em um eixo vertical que passsa por . Se um torque é aplicado à barra por meio de seu eixo, calcule a força horizontal no mancal quando a barra começa a girar.
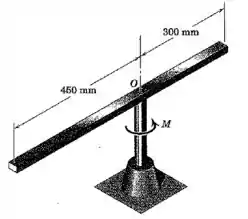
Passo 1
Vamos ver qual é a aceleração angular gerada pelo momento aplicado sobre o eixo. Para isso precisaremos do momento de inércia em relação ao eixo :
O momento de inércia de uma barra esbelta em relação ao seu centro de massa é:
Nesse caso, o centro de massa está em contando a partir de uma extremidade. Isso quer dizer que o ponto está do centro de massa, então, pelo teorema dos eixos paralelos:
Passo 2
Agora podemos calcular a aceleração angular gerada pelo momento:
E isso quer dizer que a aceleração tangencial do centro de massa, que está a do eixo é:
Como a única força agindo na direção tangencial é a força horizontal no mancal, que queremos calcular, então pela segunda lei de Newton temos que:
Resposta
A força é .