Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 80
Um tambor de de raio está rigidamente preso a um tambor de de raio como ilustra a figura. Um dos tambores rola sem deslizar sobre a superfície mostrada e uma corda é enrolada ao redor do outro tambor. Sabendo que a extremidade E da corda é puxada para a esquerda com uma velocidade de , determine (a) a velocidade angular dos tambores, (b) a velocidade do centro dos tambores e (c) o comprimento de corda enrolada ou desenrolada por segundo.
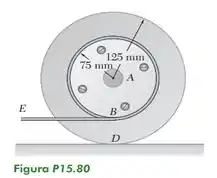
Passo 1
Questão 80 agora, meus chapas!
Bom! Vamos começar nossa resolução, fazendo um esboço do que está acontecendo em nosso problema... A chamada representação vetorial das velocidades!
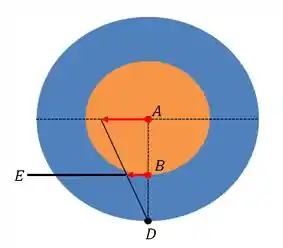
Se liga! A gente tem que...
Passo 2
a) Bom! Primeiro, vamos obter a velocidade angular. Ela é dada por
Passo 3
b) Descoberta a velocidade angular, vamos obter a velocidade no centro dos tambores, ou seja, . Ela vai ser dada por...
Passo 4
c) Por fim, para obter o comprimento de corda enrolada ou desenrolada por segundo, precisamos usar o conceito de velocidade relativa...
Fazemos isso, pois estamos analisando o movimento entre dois objetos. Para o tambor menor, temos que...
E como é maior que ! Esse é o comprimento de corda enrolada!
Feshow, meus queridos!
Resposta
a)
b)
c)