Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 33
A barra esguia e uniforme de comprimento e massa repousa contra a superfície circular, conforme mostrado. Determine a força normal no pequeno rolo e a magnitude da reação de pivô ideal em .
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede duas coisas:
i) Determinar a reação normal no ponto no rolo;
ii) Determinar o módulo da reação no apoio do tipo pivô ideal em .
Vamos começar esboçando nosso diagrama de corpo livre da barra, nela estão atuando as reações do pivô , seu peso e a reação normal à superfície que aponta para o centro do círculo.
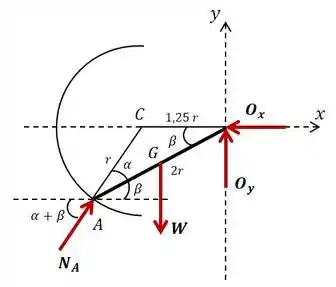
Olhando para o triângulo AOC, nós sabemos as medidas de todos os lados, então podemos usar a lei dos cossenos e a lei dos senos para determinar os ângulos internos do triângulo:
Para simplificar, vamos chamar o lado de , de e de . Usando a lei dos cossenos:
E pela lei dos senos temos:
Passo 2
Show, feito isso, ainda temos três incógnitas para encontrar: as reações , e . Para isso vamos utilizar as equações de equilíbrio.
Começando pelo momento em torno de , já que isso elimina duas das nossas incógnitas, restando apenas .
Passo 3
Show! Agora faremos o somatório de forças na direção para encontrar :
E na direção para encontrar :
Com isso, ficou fácil calcular o módulo da reação em :
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 