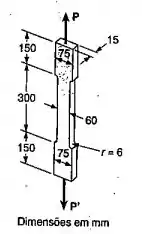
O corpo de prova de alumínio mostrado é submetido a duas forças centradas e axiais iguais e opostas, de intensidade P. Pede-se
- Sabendo-se que E=70GPa e , determinar o máximo valor admissível de P e o correspondente alongamento para a amostra total.
- Resolver o item a, considerando que o corpo de prova foi substituído por uma barra de alumínio de mesmo comprimento, mas de seção transversal retangular uniforme de
Passo 1
A barra uniforme não tem adoçamento nem concentração de tensão, o que deixa tudo mais fácil. Então vamos calcular a força de forma direta.
Primeiro calculamos a área de seção transversal:
E calculamos a força:
Isolamos o
Logo:
Passo 2
E agora é só calcular a deformação:
Aplicamos os valores:
E chegamos na deformação