Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 90

O cubo do problema 2.89, de um material compósito, é impedido de se deformar na direção z e é alongado na direção x em 0,035 mm por uma força de tração na direção x. Determine (a) as tensões σ x ,     σ y e σ z e (b) a variação na dimensão do cubo na direção y.

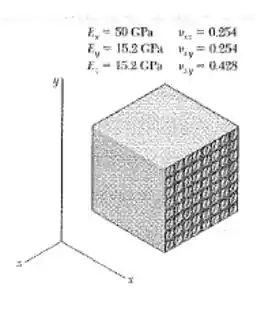
Passo 1

Nós temos do enunciado

E x = 50   G P a

E y = 15,2   G P a

E Z = 15,2   G P a

v x z = 0,254

v x y = 0,254

v z y = 0,428

Essa questão é um pouco mais complexa. As equaç~es que vamos ter para montar um sisteminha serão

1   ϵ x = σ x E x - v y x σ y E y - v z x σ z E z

2   ϵ y = - v x y σ x E x + σ y E y - v z y σ z E z

3 ϵ z = - v x z σ x E x - v y z σ y E y + σ z E z

Temos ainda que

4 v x y E x = v y x E y

5 v y z E y = v z y E z

6 v z x E z = v x z E x

Passo 2

Do enunciado temos que o cubo é impedido de se deformar na direção z, logo

ϵ z = 0

Temos ainda a condição de carga

σ y = 0

Da enquação (3) então temos.

0 = - v x z E x σ x + 1 E z σ z

σ z = v x z E z E x σ x = 0,254 15,2 50 = 0,077216 σ x

Passo 3

A partir da equação (1) com σ y = 0

ϵ x = 1 E x σ x - v z x E z σ z = 1 E x σ x - v x z E x σ z

ϵ x = 1 E x σ x - 0,254 σ x

ϵ x = 1 E x 1 - 0,254 0,077216 σ x  

σ x = E x ϵ x 0,98039

Mas devemos lembrar ainda que

δ x = ϵ x L x

ϵ x = δ x L x = 0,035   m m 40   m m = 875 × 10 - 6

Passo 4

Para a letra (a) teremos então

σ x = 50 × 10 9 875 × 10 - 6 0,98039 = 44,625 × 10 3 P a = 44,6   M P a

σ y = 0

σ z = 0,077216 44,625 × 10 6 = 3,446 × 10 6 P a = 3,45   M P a

Apartir da equação 2 entçao teremos

ϵ y = - v x y E x σ x + 1 E y σ y - v z y E z σ z

= - 0,254 44,625 × 10 6 50 × 10 9 + 0 - 0,428 3,446 × 10 6 15,2 × 10 9

= - 323,73 × 10 - 6

E para a (b) teremos

δ y = L y ϵ y = 40 m m - 323,73 × 10 - 6 = - 0,0129   m m

Resposta

a )   σ x = 44,6   M P a

σ y = 0

σ z = 3,45   M P a

b )   δ x = - 0,0 129   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra uniforme de 9,5m m de diâmetro e 2,7m de comprimento é feita de um aço inoxidável de alta resistência, para o qual σ e = 860M P a e E = 190G P a .Sabendo-se que uma energia de deformação de
Uma barra A B de 6m m de diâmetro, com comprimento L = 2,5m é feita de uma liga de alumínio para a qual σ e = 320M P a e E = 72G P a . Sabendo-se que uma energia de deformação de 10J deve ser absorvid
Resolver o Prob. 10.19, assumindo que a = 635m m .
A barra A B C é feita de aço ára o qual σ e = 350M P a e E = 200G P a . Sabendo-se que uma energia de deformação de 4,5N ⋅ m deve ser acumulada pela barra assim que a carga axial P é aplicada, determi
Cada uma das barras mostradas é feita de um aço com tensão de escoamento igual a σ e = 250M P a e o módulo de elasticidade de E = 200G P a . Sabendo-se que l = 380m m , determinar a máxima energia de