Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 92
Sabendo-se que a tensão normal admissível para o aço da barra mostrada vale 150 MPa, determinar a máxima força P admissível, axial e centrada, que pode ser aplicada à barra.
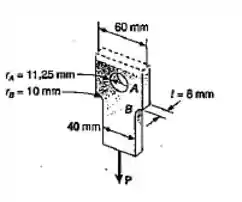
Passo 1
Para começar vamos anotar os dados que nós temos:
Encontrando primeira mente a relação entre temos
Temos ainda que
Encontramos pela tabela então que
Passo 2
Uma vez que possuímos o k, temos a relação
Para calcularmos o A fazemos
Passo 3
Temos então a relação
Passo 4
Para o adoçamento fazemos um passo a passo similar. Vou fazer as contas um pouco mais rapidinho.
Encontramos na tabela então que
Por ultimo então temos
Resposta
Exercícios de Livros Relacionados
Usando E = 200G P a , determinar:a energia de deformação da barra de aço A B C , quando P = 60k N ;a correspondente densidade de energia de deformação nas porções A B e B C da barra.
O diagrama tensão-deformação mostrado foi desenhado a partir dos dados obtidos durante um ensaio de tração de um corpo de prova de uma liga de alumínio. Usando E = 72G P a , determinar:o módulo de res
O diagrama carga-deformação mostrado foi desenhado a partir dos dados obtidos durante um ensaio de tração de um corpo de prova de uma liga de alumínio. Sabendo-se que a área da seção transversal do C
Uma porção de uma barra de aço quadrada, de 22m m de lado, foi usinada produzindo um cilindro de diâmetro 22m m , como mostrado. Sabendo-se que a tensão normal admissível do aço é σ a d m = 150M P a e
Resolver o Prob. 10.14, usando as propriedades do material dado e assumindo que a barra A B C é feita inteiramente de:aço;alumínio.