Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 49

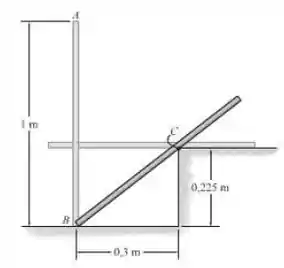
A barra fina uniforme AB, de 6 kg, é submetida a uma ligeira perturbação horizontal quando está na posição vertical e gira em torno de B sem deslizar. Subsequentemente, ela atinge o degrau em C. O impacto é perfeitamente plástico e, assim, a barra gira em torno de C sem deslizar após o impacto. Determine a velocidade angular da barra quando ela está na posição horizontal mostrada.

Passo 1

A partir da geometria, θ =   tan - 1 ⁡ 0,225 0,3 = 36,87 º e BC = 0,3 2 + 0,225 2 = 0,375   m .   Então, r c g = 0,5 – 0,375 = 0,125 m. Com a referência, V 1 = W ( y g 1 )   = 6(9,81)(0,5) = 29,43 J, V 2 = V 3 = W ( y g 3 )   = 6(9,81)(0,5.sen(36,87º)) = 17,658 J e V 4 = W ( y g 4 )   = 6(9,81)(0,225) = 13,2435 J.

Como a haste está inicialmente em repouso, T 1 = 0. A haste gira em torno do ponto B antes do impacto. Assim, v g 2 =   w 2 r b g = w 2 0,5 . O momento de inércia da haste em torno de seu centro de massa é:

I g = 1 12 m l 2 = 1 12 6 1 2 = 0,5   k g . m ²

Portanto,

T 2 = 1 2 m v g 2 2 + 1 2 I g w 2 = 1 2 6 [ w 2 ( 0,5 ) ] 2 + 1 2 0,5 w 2 = 1 w 2 2

Assim,

T 1 + V 1 = T 2 + V 2

0 + 29,43 =   1 w 2 2 + 17,658

w 2 = 3,431   r a d / s

Passo 2

A haste gira em torno do ponto C após o impacto. Então, v g =   w r c g = w 0,125 . Portanto,

T = 1 2 m v g 2 + 1 2 I g w 2 = 1 2 6 [ w 0,125 ] 2 + 1 2 0,5 w 2 = 0,29687 w ²

Então,

T 3 = 0,29687 w 3 ² e T 4 = 0,29687 w 4 ²

T 1 + V 1 = T 2 + V 2

0,29687 w 3 2 +   17,658 =   0,29687 w 4 2 + 13,2435

w 4 2 - w 3 2 = 14,87

Resposta

A soma dos impulsos angulares em torno do ponto C é zero. Assim, o momento angular da haste é conservado nesse ponto durante o impacto.

H C 1 = ( H C ) 2

6 3,431 0,5 0,125 + 0,5 3,431 = 6 w 3 0,125 0,125 + 0,5 w 3

w 3 = 5,056   r a d / s

Substituindo na equação anterior,

w 4 2 - ( 5,056 ) ² = 14,87

w 4 = 6,36   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As esferas de 0,5 kg de um regulador centrífugo giram a uma velocidade escalar constante v no círculo horizontal de 0,15 m de raio, tal como mostra a figura. Desprezando a massa das hastes AB, BC, AD
Resolva o problema 12.28, assumindo que m A = 5 k g , m B = 10 k g e m C = 20 k g
Um trecho de uma pista de tobogã mostrada na figura está contido em um plano vertical. As seções AB e CD têm raios de curvatura com indicado e a seção BC é uma linha reta e forma um ângulo de 20° com
Durante uma corrida de alta velocidade, um carro esportivo de 1200 kg que viaja a uma velocidade escalar de 160 km/h perde, por um instante, o contato com a estrada quando ele atinge o cume A de um mo
Uma criança de massa 22 kg está sentada em um balanço e sendo mantida na posição mostrada na figura por uma segunda criança. Desprezando o peso do balanço, determine a tração no cabo AB (a) enquanto a