Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 36

A empilhadeira se desloca para frente com uma velocidade constante de 2,7 m/s. Determine a distância de parada mais curta sem fazer com que nenhuma das rodas deixe o solo. A empilhadeira tem massa de 1000 kg com centro de gravidade em G 1 e a carga pesa 4500 N ( ≈ 450   k g ) com centro de gravidade em G 2 . Despreze o peso das rodas.

Passo 1

Para resolver esse exercício, vamos analisar o caso limite, onde as rodas estão na iminência de deixar o solo, para analisar qual seria a maior aceleração de frenagem e consequentemente a menor distância percorrida até a parada. Usaremos o seguinte diagrama de corpo livre como referência:

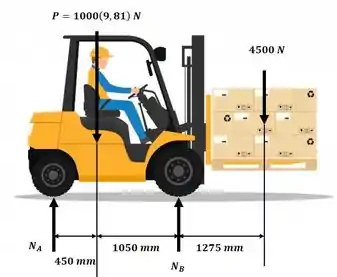
Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².

Passo 2

No caso limite, com as rodas prestes a saírem do chão, temos N A = 0 . Sendo assim, aplicando somatório de momento em torno do ponto B, temos:

↺ + ∑ M B = M k B

1000 9,81 1,05 - 4500 1,275 = 1000 a G 0,6 + 450 a G ( 0,975 )

a G = 4,393   m / s 2

Passo 3

Agora, considerando a aceleração de frenagem constante, podemos encontrar a distância de frenagem através da equação de Torricelli:

v 2 = v 0 2 + 2 a G ∆ s

Lembrando que a aceleração é negativa, pois vai contra o movimento inicial da empilhadeira.

0 2 = 2,7 2 + 2 - 4,393 ∆ s

∆ s = 0,830   m

Resposta

∆ s = 0,830   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A roda de 150 kg tem um raio de giração em relação a seu centro de massa O de k O = 250 mm. Se ela gira no sentido anti-horário com uma velocidade angular ω = 1200 rev/min no instante em que as forças
Determine a aceleração angular do trampolim de 25 kg e as componentes verticais e horizontais da reação no pino A no instante em que o homem realiza o salto. Suponha que a tábua do trampolim seja unif
A barra uniforme de 50 kg está em repouso em uma posição vertical quando a corda fixada a ela em B é submetida a uma força P = 250 N. Determine a aceleração angular inicial da barra e a intensidade da
Inicialmente, a roda A gira no sentido horário com uma velocidade anular constante de ω = 100 rad/s. Se A é colocada em contato com B, que é mantida fixa, determine o número de revoluções antes que a
A barra fina uniforme tem uma massa de 9 kg. Se a mola está distendida quando θ = 0°, determine a intensidade da força reativa exercida sobre a barra pelo pino A quando θ = 45°, se, nesse instante, ω