Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 47

Um trecho de uma pista de tobogã mostrada na figura está contido em um plano vertical. As seções AB e CD têm raios de curvatura com indicado e a seção BC é uma linha reta e forma um ângulo de 20° com a horizontal. Sabendo que o coeficiente de atrito cinético entre o trenó e a pista é 0,10 e que a velocidade escalar do trenó é 7 m/s em B, determine a componente tangencial da aceleração do trenó (a) exatamente antes dele alcançar B, (b) exatamente depois dele passar por C.

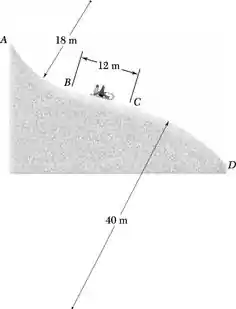
Passo 1

Vamos analisar o desenho do enunciado, pouco antes de B, ρ = 18   m certo? Sabemos que a força é dada por:

+ ↗ Σ F n = m a n

        N - W cos ⁡ 20 ° = W g v B 2 ρ 2

Isolando N temos:

N = W cos ⁡ 20 ° + v B 2 g ρ B

Como está deslizando consideramos o atrito:

F = μ n N

= μ k W cos ⁡ 20 ° + v B 2 g ρ B

+ ↘ Σ F t = m a t :         W sin ⁡ 20 ° - F = W g a t

Isolando a aceleração

a t = g sin ⁡ 20 ° - μ t cos ⁡ 20 ° - μ k v B 2 ρ B

Agora basta substituirmos

a t = 10 sin ⁡ 20 ° - 0.1 cos ⁡ 20 ° - 0.1 7 18 = 2,44   m / s ²

Passo 2

É necessário primeiro determinar vc.

Para a seção BC

+ ↗ Σ F y = 0 :         N B C - W cos ⁡ 20 ° = 0

ou

N B C = W cos ⁡ 20 °

Deslizante:

F B C = μ k N B C = μ k W cos ⁡ 20 °

+ ↘ Σ F x = m a B C :       W sin ⁡ 20 ° - F B C = W g a B C

Isolando a aceleração temos:

a B C = g sin ⁡ 20 ° - μ k cos ⁡ 20 °

= 10 sin ⁡ 20 ° - 0.1 cos ⁡ 20 ° = 2,48 m s ²

Passo 3

Agora logo depois C, ρ C = 40   m

+ ↙ Σ F n = m a n :         W cos ⁡ 20 ° - N W g v C 2 ρ C

ou

N = W cos ⁡ 20 ° - v C 2 g ρ C

Passo 4

Deslizando:

F = μ k N

= μ k W cos ⁡ 20 ° - v C 2 g ρ C

+ ↘ Σ F t = m a t :         W sin ⁡ 20 ° - F = W g a t

ou

a t = g sin ⁡ 20 ° - μ k cos ⁡ 20 ° + μ k v C 2 ρ C

Nota:

g sin ⁡ 20 ° - μ k cos ⁡ 20 ° = a B C

Isolando a aceleração e substituindo temos que:

a t = 2,48 + 0.1   10.83625 40 = 2,5   m / s ²

Resposta

a)   a t = 2,48 m s ²     20 °

b)   a t = 2,5   m / s 2     20 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O vagão-plataforma de 25t suporta um veículo de 7,5t em uma rampa de 5 ° construída sobre o vagão-plataforma. Se o veículo é liberado a partir do repouso com o vagão-plataforma também em repouso, dete
Uma partícula de 0,5k g sofre a ação da força F = 2 t 2 i - 3 t + 3 j + 10 - t 2 kN , onde t está em segundos. Se a partícula tem uma velocidade inicial de v 0 = 5 i + 10 j + 20 km / s , determine a i
O bloco deslizante de 40k g move-se para a direita com uma velocidade de 1,5m / s quando atuam sobre ele as forças F 1 e F 2 . Se essas cargas variam da maneira mostrada no gráfico, determine a veloci
O guincho transmite uma força de reboque horizontal F ao seu cabo em A , que varia como mostrado no gráfico. Determine a velocidade do balde de 8 0k g quando t = 24s . Originalmente o balde é solto do
O trem consiste de uma locomotiva E de 30M g e dos vagões A ,B e C , que têm massas de 15M g , 10M g e 8M g , respectivamente. Se os trilhos proporcionam uma força de tração de F = 30k N às rodas da l