Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 51

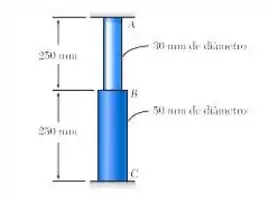
Uma barra formada por duas partes cilíndricas AB e BC está impedida de se deslocar em ambas as extremidades. A parte AB é feita de aço ( E a ç o = 200   G P a ,     a a ç o = 11,7   x   10 - 6 / ° C ) e a parte BC é feita de latão ( E l a t a o = 105   G P a ,     a a ç o = 20,9   x   10 - 6 / ° C ) . Sabendo que a barra está inicialmente livre de tensões, determine a força compressiva induzida em ABC quando há um aumento de temperatura de 50°C.

Passo 1

Fala aí gurizada tudo belezinha? Para determinarmos a força compressiva induzida em ABC, antes precisamos determinar a área das regiões do elemento, vejam um esboço de como as forças agem neste elemento, partiu!!!

Calculando a área das seções temos:

A A B = π 4 d A B 2 = π 4 30 2 = 706,86   m m ² = 706,86   x   10 - 6 m ² A B C = π 4 d B C 2 = π 4 50 2 = 1,9635   x   10 3 m m ² = 1,9635   x   10 - 3 m ²

E a expansão térmica temos.

δ T = L A B α s   x   ∆ T +   L B C α b   x   ∆ T = 0,250   x   11,7   x   10 - 6   x   50 + 0 , 25 0   x   20,9   x   10 - 6   x   50 = 3,075 × 10 - 4   m

Encurtamento devido à força compressiva é dada por:

δ P = P L E s A A B + P L E b A B C

Substituindo os valores temos:

= 0,250 P 200   x   10 9   x   706,86   x   10 - 6 + 0,250 P 105   x   10 9   x   1,9635   x   10 - 3

= 2,98   x   10 - 9 P

Para deflexão total consideramos que, δ P = δ T 2,98   x   10 - 9 P = 3,075 × 10 - 4 P = 103,2   k N

Obs: Talvezz tenha reparado que o resultado está diferente da resposta no final do livro. Mas isso deve ser um erro da tradução para português. Na versão em inglês o L B C é 300 mm. Se fizer com esse valor dá certinho o valor que está na resposta no final do livro.

Resposta

P = 103,2   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

σ E = 448 M P a . Usando o critério da máxima energia de distorção, determine o intervalo de valores de σ y para o qual o coeficiente de segurança associado à tensão de escoamento é igual ou maior do
O estado de tensão mostrado na figura ocorre em um componente de máquina feito de um tipo de aço para o qual σ E = 448M P a . Usando o critério da máxima energia de distorção, determine o coeficiente
Determine a energia de deformação da viga prismática AB, levando em conta o efeito das tensões normal e de cisalhamento
σ E = 160 M P a . Usando o critério da máxima energia de distorção, determine se ocorre o escoamento quando (a) σ z = + 45M P aeb σ z = - 45M P a
O bloco cilíndrico E de 18 lb tem uma velocidade horizontal v 0 quando atinge diretamente o batente BD que está conectado às hastes AB e CD com diâmetro de 1 8 _ = i n . Sabendo que as hastes são feit