Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 38

σ E = 448   M P a . Usando o critério da máxima energia de distorção, determine o intervalo de valores de σ y para o qual o coeficiente de segurança associado à tensão de escoamento é igual ou maior do que 2,2.

Passo 1

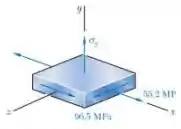
O enunciado pede que a gente determine o intervalo de valores de σ y para o qual o coeficiente de segurança associado à tensão de escoamento é igual ou maior do que 2,2.

σ a v e = 1 2 0 + 8 = 4   k s i

σ x - σ z 2 = 8 - 0 2 = 4   k s i

Passo 2

Onde:

τ x z = 14   k s i

R σ x - σ z 2 2 + τ x z 2 = 4 2 + 14 2 = 14,56   k s i

σ a = σ a v e + R = 18,56   k s i

σ b = σ a v e - R = - 10,56   k s i

Passo 3

Consideramos que:

σ c = σ y

σ a - σ b 2 + σ b - σ c 2 + σ c - σ a 2 = 2 σ Y F . S . 2

18,56 + 10,56 2 + - 10,56 - σ Y 2 + σ y - 18,56 2 = 2 65 2,2 2

847,97 + 111,51 + 21,12 σ y + σ y 2 + σ y 2 - 37,12 σ y + 344,47 = 1745,87

2 σ y 2 - 16 σ y - 441,92 = 0

Isolando σ y temos:

σ y = 16 ± 16 2 + 4 2 441,92 2 2 = 4 ± 15,39

σ y = 19,39   k s i ,   - 11,39   k s i

- 11,39   k s i   ≤ σ y   ≤ 19,39   k s i

Resposta

- 11,39   k s i   ≤ σ y   ≤ 19,39   k s i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine (a) a força de compressão nas barras mostradas depois que a temperatura atingiu 82°C e (b) a variação correspondente no comprimento da barra de bronze.
Determine a força P máxima que pode ser aplicada à barra de latão do Problema 2.55 se a tensão admissível nas barras de aço for de 30 MPa e a tensão admissível na barra de latão, 25 MPa.
Uma barra formada por duas partes cilíndricas AB e BC está impedida de se deslocar em ambas as extremidades. A parte AB é feita de latão ( E l a t a o = 29x10 6 p s i ,a l a t ã o = 6,5x10 - 6 / ° F )
Um tubo de latão ( a l a t ã o = 11,6x10 - 6 / ° F ) ã é totalmente preso ao núcleo de aço ( a a ç o = 6,5x10 - 6 / ° F ) ç . Determine o maior aumento permitido na temperatura considerando que a tens
Sabendo que existe um espaçamento de 0,508 mm quando a temperatura é de 23,9°C, determine (a) a temperatura na qual a tensão normal na barra de alumínio será igual a -75,8 MPa e (b) o comprimento exat