Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 40

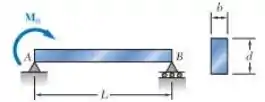
Determine a energia de deformação da viga prismática AB, levando em conta o efeito das tensões normal e de cisalhamento

Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente Determine a energia de deformação da viga prismática AB, para isso vamos trazer os valores das reações e do esforço cortante :D

Reações:

R A = M 0 L ↓ ,     R B = M 0 L ↑

Esforço cortante:

V = M 0 L

O momento é:

M = M 0 L v

Passo 2

Agora gurizada por integral vamos encontrar a energia de deformação da viga prismática, considere os limites de integração de 0 a L :D

U 1 = ∫ 0 L M 2 2 E I d v = M 0 2 2 E I L 2 ∫ 0 L v 2 d v = M 0 L 3 6 E I L 2 = M 0 2 L 6 E I

A tensao de cisalhamento é dada por:

τ x y = 3 2 V A 1 - y 2 c 2     c = 1 2 d

u = τ x y 2 2 G = 9 V 2 8 G A 2 1 - y 2 c 2 2 = 9 M 0 2 8 G b d 2 L 2 1 - 2 y 2 c 2 + y 4 c 4

Passo 3

Agora a energia de ativação “2” é obtida também por integram como:

U 2 = ∫ u d v = ∫ 0 2 = 9 M 0 2 b 8 G b 2 d 2 L 2 ∫ 0 L ∫ - c c 1 - 2 y 2 c 2 + y 4 c 4 d y   d x

= 9 M 0 2 8 G b d 2 L 2 ∫ 0 2 y - 2 3 y 3 c 2 + 1 5 y 5 c 4 - c c d x = 9 M 0 2 8 G b d 2 L 2 ∫ 0 L 2 c - 4 3 c + 2 5 c d x

9 M 0 2 8 G b d 2 L 2 16 15 c L = 6 5 M 0 2 C G B d 2 L = 3 5 M 0 2 G b d L

Passo 4

Agora sim gurizada podemos ter a energia total somando as energias obtidas nos passos anteriores:

Total:

U = U 1 + U 2 = M 0 2 L 6 E I + 3 5   M 0 2 G b d L

Sendo a inercia obtida por:

I = 1 12 b d 3

U = 2 M 0 2 L E b d 3 + 3 5 M 0 2 G b d L                                        

  U = 2 M 0 2 L E b d 3 1 + 3 E d 2 10 G L 2

Resposta

U = 2 M 0 2 L E b d 3 1 + 3 E d 2 10 G L 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a barra composta do Problema 2.111, determine as tensões residuais nas barras de aço temperado se P for gradualmente aumentada até zero até a deformação da barra atingir um valor máximo δ m = 1,0
Para a barra composta do Problema 2.111, determine as tensões residuais nas barras de aço temperado se P for gradualmente aumentada de zero até 436k N e depois diminuída novamente até zero.
Resolva o Problema 2.117 considerando que a temperatura da barra é incrementada até 150°C e depois reduzida até 25°C.
A barra AB tem uma área de seção transversal de 120 mm² e é feita de um aço elastoplástico com E = 200G P aeσ E = 250M P a . Sabendo que a força F aumenta de 0a250k N e depois diminui para zero, deter
Resolva o Problema 2.122, considerando que a = 180m m .