Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 108
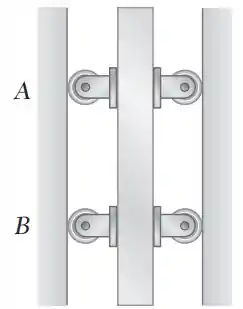
Uma barra de massa m é mantida, como mostra a figura, entre quatro discos, cada um de massa m' raio r = 75 mm. Determine a aceleração da barra imediatamente depois dela ter sido liberada do repouso, sabendo que as forças normais nos discos são suficientes para evitar qualquer escorregamento e considerando que (a) m'= 5 kg e m'= 2 kg, (b) a massa m' dos discos é desprezada, (c) a massa m da barra é desprezada.
Passo 1
Cinematica:
Disco está rolando na parede vertical
Cinética da barra
(1)
Cinética de um disco
(2)
Passo 2
Substituindo para F da (2) na (1).
(a)
Passo 3
(b)
(c)
Resposta
(a)
(b)
(c)
Exercícios de Livros Relacionados
Uma pequena braçadeira de massa mB está presa em B a um arco de massa mh. Sabendo que o sistema é liberado a partir do repouso e rola sem deslizar, deduza uma expressão para a aceleração angular do ar
A metade da seção do cilindro uniforme de massa m está em repouso quando a força P é aplicada como mostra a figura. Considerando que a seção rola sem deslizamento, determine (a) sua aceleração angular
Uma barra de 2 kg é ligada a um cilindro uniforme de 5 kg por um pino quadrado P, como mostrado na figura. Sabendo que r = 0,4 m, h = 0,2 m, θ = 20°, L = 0,5 m eω = 2 rad /s no instante mostrado, dete
As extremidades da haste uniforme AB de 2 kg são presas a cursores de peso desprezível que deslizam sem atrito ao longo de hastes fixas mostradas na figura. Se haste AB é liberada do repouso na posiçã
O movimento da haste uniforme AB de massa 5 kg e comprimento L = 750 mm é guiado por pequenas rodas de massa desprezível que rolam sobre a superfície mostrada na figura. Se a haste é liberada a partir