Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 116

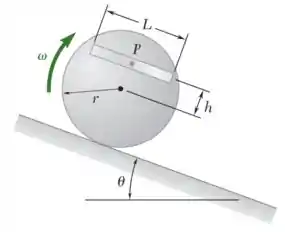
Uma barra de 2 kg é ligada a um cilindro uniforme de 5 kg por um pino quadrado P, como mostrado na figura. Sabendo que r = 0,4 m, h = 0,2 m, θ = 20°, L = 0,5 m e   ω =   2 rad /s no instante mostrado, determine as reações em P neste instante considerando que o cilindro rola para baixo sem deslizar no plano inclinado.

Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente determine as reações em P neste instante considerando que o cilindro rola para baixo sem deslizar no plano inclinado

Massas e momentos de inercia.

Barra:

m B = 2 k g I - B = 1 12 m B L 2 = 1 12 ( 2 ) ( 0.5 ) 2 = 0.04167 k g ⋅ m 2

Disco:

m D = 5 k g I ~ D = 1 2 m C r 2 = 1 2 ( 5 ) ( 0.4 ) 2 = 0.4 k g ⋅ m 2

Passo 2

Cinemática. Deixe o Ponto C ser o ponto de contato entre o cilindro e a inclinação e o Ponto G ser o centro de massa do cilindro sem a barra. Assume que o centro de massa da barra fica no Ponto P.

α = α ∞ ⋅ a G = a G   ∢   20 ∘

Para rolar sem escorregar,

a C t = a G - r α = 0 a G = r α a p t = a G + h α a P t = ( r + h ) α a p h = 0 + h ω 2 = h ω 2

Passo 3

Cinética: Usando o cilindro mais a barra como um corpo livre.

+ ) Σ M C = + Σ M C e f f : m D g r ⋅ s e n ⁡ θ + m B ( r + h ) s e n ⁡ θ = I - D α + m D a G r + I - B α + m B a P i ( r + h ) = I - D + m D r 2 + I - B + m B ( r + h ) 2 α α = m D r + m B ( r + h ) g s e n ⁡ θ I - D + m D r 2 + I - B + m B ( r + h ) 2 = [ ( 5 ) ( 0.4 ) + ( 2 ) ( 0.6 ) ] ( 9.81 ) s e n ⁡ 20 ∘ 0.4 + ( 5 ) ( 0.4 ) 2 + ( 0.04167 ) + ( 2 ) ( 0.6 ) 2 = 5.4732 r a d / s 2 a P t = ( 0.6 ) ( 5.4732 ) = 3.2840 m / s 2 a p n = ( 0.2 ) ( 2 ) 2 = 0.8 m / s 2

Passo 4

Usando a barra sozinha como corpo livre,

+ ⃑ ∑ F x = Σ F x e f f :                                                 P x = m B a P t c o s ⁡ 20 ∘ - m B a p n s e n ⁡ 20 ∘ = ( 2 ) ( 3.2840 ) c o s ⁡ 20 ∘ - ( 2 ) ( 0.8 ) s e n ⁡ 20 ∘ P x = 5.625 N ± ↑ Σ F y = Σ F y e f f : P y - m B g = - m B a P t s e n ⁡ 20 ∘ - m B a P n c o s ⁡ 20 ∘ P y = ( 2 ) ( 9.81 ) = - ( 2 ) ( 3.2840 ) s e n ⁡ 20 ∘ - ( 2 ) ( 0.8 ) c o s ⁡ 20 ∘ P y = 15.87 N P = 5.625 2 + 15.87 2 = 16.84 N t a n ⁡ β = 15.87 5.625 β = 70.5 ∘

± )   Σ M P = Σ M P e f f :                           M P = I - D α

= ( 0.04167 ) ( 5.4732 )

Resposta

P = 16.84 N   ∢   70.5 ∘  

M P = 0.228   N ∙ m )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2. O volante gira com uma velocidade angular de ω = 0,005 θ 2 r a d / s , onde θ é dado em radianos. Determine a aceleração angular quando ele girou 20 revoluções.
3. O volante gira com uma velocidade angular de =4 θ 1 2 rad/s, onde é dado em radianos. Determine o tempo que ele leva para alcançar uma velocidade angular de =150 rad/s. Quando t=0, θ=0.
4. O balde é içadoo pela corda que se enrola em torno do tambor. Se o deslocamento angular da roda é θ = 0,5 t 3 + 15 t r a d ,onde t é dado em segundos, determine a velocidade e aceleração do balde q
6. Por um curto período de tempo, o motor gira a engrenagem A com uma aceleração angular constante aA=4,5rads2 , partindo do repouso. Determine a velocidade do cilindro e a distância que ele se desloc
1. Quando a engrenagem gira 20 revoluções, ela alcança uma velocidade angular ω=30rads , partindo do repouso. Determine sua aceleração angular constante e o tempo necessário.