Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 122

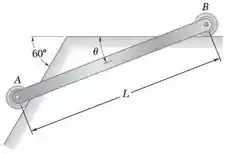
O movimento da haste uniforme AB de massa 5 kg e comprimento L = 750 mm é guiado por pequenas rodas de massa desprezível que rolam sobre a superfície mostrada na figura. Se a haste é liberada a partir do repouso quando θ = 20°, determine (a) a aceleração angular da haste, (b) a reação em A.

Passo 1

O exercício pede que a gente determine (a) a aceleração angular da haste, (b) a reação em A.

Cinemática:

a B = a A + a B / A

a B ← = a A     60 ° + L α     20 °

Passo 2

Lei dos senos:

a A s i n s i n   70 °   = a B s i n s i n   55 °   = L α s i n s i n   60 °  

a A = 1.0851 L α     70 °

a B = 0.88455 L α ←

a G / A = L 2 α   20 °

a G = a _ = a A + a G / A = 1.0851 L α     60 ° + L 2 α     20 °

  + ←   a _ x = 1.0851 L α c o s c o s   60 ° + 0.5 L α s i n s i n   20 °    

= 0.54254 L α + 0.17101 L α ;             a _ x = 0.71355 L α ←

  + ↓   a _ y = 1.0851 L α s i n s i n   60 ° + 0.5 L α c o s c o s   20 °    

= 0.93972 L α - 0.46985 L α ;             a _ y = 0.46985 L α ↓

Passo 3

Nós temos:

a _ x = 0.71355 L α   ←

a _ y = 0.46985 L α   ↓

Passo 4

Triângulo ABE:

∠ A B E = 70 °

∠ A B E = 70 ° ,   ∠ B A E = 50 °

Lei dos senos:

A B = L

B E s i n s i n   50 °   = L s i n s i n   60 °   ;                 B E = 0.88455 L

Passo 5

  1. Aceleração angular.

    2. + Σ M E = Σ M E e f f :               m g 0.46985 L = I _ α + m a _ x 0.71355 L + m a _ y 0.46985 L

    0.46985 m g L = 1 12 m L 2 α + m 0.71355 L α 0.71355 L

    + m 0.46985 L α 0.46985 L

    0.46985 m g L = m L 2 0.81325 α

    α = 0.57775 g L = 0.57775 9.81   m / s 2 0.75   m

    = 7.557   r a d / s 2

    Passo 6

  2. Reação em A.

  + ←   Σ F x = Σ F x e f f :               A s i n s i n   60 ° = m a x = m 0.71355 L α  

A s i n s i n   60 ° = 5   k g 0.71355 0.75   m 7.557   r a d / s 2 = 32.354  

A = 23.349   N

Resposta

a )   α = 7.45   r a d / s 2  

b )   A = 23.3   N     30 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3. O gancho está preso a uma corda que está enrolada em torno do tambor. Se ele desloca do repouso com uma aceleração de 6 m/ s 2 , determine a aceleração angular do tambor e sua velocidade angular ap
12. Se o motor da furadeira elétrica gira o eixo do induzido S com uma aceleração angular constante de a s = 30r a d / s 2 , determine a velocidade angular do eixo após ele ter girado 200 revolucoes,
16. Se a polia A de 50 mm do motor da secadora de roupas gira com uma aceleração angular a A = 10 + 50 t r a d s 2 , onde t é dado em segundos, determine sua velocidade angular quando t =3s, partindo
13. Se o motor da furadeira elétrica gira o eixo do induzido S com uma velocidade angular de ω s = ( 100 t 1 2 )r a d / s , determine a velocidade angular e aceleração angular do eixo no instante que
1. Um disco com um raio de 0,15m gira com uma velocidade angular inicial de 2 rad/s e tem uma aceleração angular constante de 1 rad/ s 2 . Determine as intensidades de velocidades e aceleração de um p