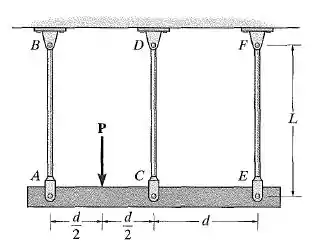
As três barras de suspensão são feitas do mesmo material e têm áreas de seção transversal iguais, . Determine a tensão normal média em cada barra se a viga rígida for submetida à força .

Diagrama de corpo livre:

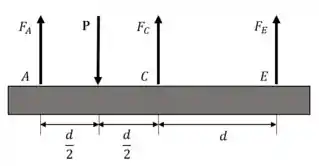
Agora vamos pras condições de equilíbrio. Primeiro, equilíbrio de forças:

Façamos o equilíbrio de momentos ao redor do ponto , tomando anti-horário como positivo:

Três incógnitas e duas equações, precisamos de mais uma relação para poder continuar.

Bora pensar na equação de compatibilidade de deslocamento.

A força não está agindo de forma simétrica, ela está à esquerda do centro de massa (ponto ) da barra. Como a viga é rígida, ela não se deforma, ou seja, ACE permanece sempre reta.

Como a força atua a esquerda do centro de massa e a viga é sempre reta, maior parcela dessa força é resistida pelos cabos A e C, por isso eles se deformam mais que o cabo em E.

E como a viga não se deforma, para que haja mais deformação nos cabos da esquerda do que nos cabos da direita, ela vai ficar inclinada. Aí com isso, temos esse antes e depois da barra rígida:

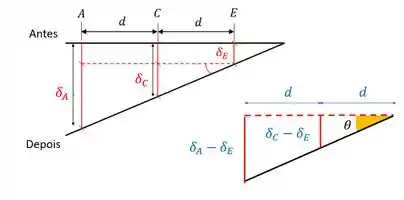
Temos dois triângulos ali com um ângulo em comum. Podemos montar uma equação com os deslocamentos das barras usando a tangente do ângulo:

Lembrando da fórmulinha da relação carga-deslocamento:

Vamos reescrever nossa equação dos deslocamentos com ela:

A área da seção das barras e o comprimento delas é o mesmo para todas das barras. O módulo de elasticidade também é o mesmo porque as barras são feitas do mesmo material. Então podemos simplificar

Essa é a nossa terceira equação! Agora dá para achar as forcinhas!

Temos esse sistema para resolver:

Substituindo em , achamos:

Substituindo essas duas relações na equação , encontramos

Voltando em , a gente acha

E substituindo isso e em , temos:

Agora que sabemos as forças e a área , é usar a fórmula da tensão:

Aí essa fórmula para cada valor de fica: