Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 34
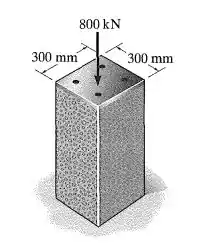
A coluna de concreto é reforçada com quatro hastes de aço, cada uma com diâmetro de . Determine a tensão no concreto e no aço se a coluna for submetida a uma carga axial de . E a, .
Passo 1
Cara, fala aí!
Vamos entender o que está acontecendo, belezinha? Temos um bloco de concreto e dentro dele a gente tem hastes de aço. Esses 5 componentes vão resistir a essa força aplicada juntos.
Por isso, vamos fazer o DCL:
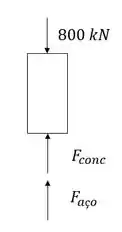
Mas queremos a tensão, que é dada por
Essa área aí a gente acha. Mas e , que é a força no concreto e nas hastes? Serão exatamente as forças de reação gerada nesses componentes. Então bora lá achar essas forças!
Passo 2
Para isso, podemos utilizar a fórmula do equilíbrio no eixo :
Temos duas variáveis e uma equação. Precisamos achar mais uma, para ter informações suficientes para ter a solução, ok?
Passo 3
Aí, temos que na geometria do alongamento. Como as hastes estão dentro do concreto, e juntos, eles formam uma só coluna, as hastes precisam ter o mesmo comprimento do bloco sempre.
Isso quer dizer que eles tem sempre o mesmo alongamento
Com isso, podemos aplicar a fórmula do alongamento para cada componente:
Lembrando ali de tirar as áreas das seções do aço de dentro da seção quadrada do concreto.
Voltando para o que a gente achou antes
Prontinho, achamos mais uma equação!
Passo 4
Resolvendo este sistema linear,
Temos:
Agora, basta substituirmos:
Para o alumínio, temos: