Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 180
Uma conexão de aço tem a seção transversal mostrada e os furos estão dispostos segundo o ângulo central . Sabendo-se que a tensão admissível é de , determinar a maior força P que pode ser aplicada quando
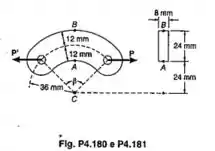
Passo 1
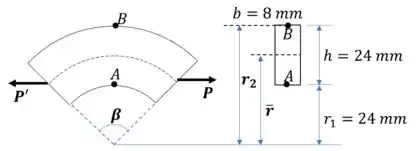
Primeiro vamos calcular algumas propriedades da seção.
A área de seção transversal:
O raio externo:
O raio até o centroide:
Agora vamos calcular o raio de curvatura da linha neutra:
Logo, a excentricidade entre linha neutra e centroide é:
Passo 2
O maior esforço vai ocorrer no centro da viga. Vamos utilizar isso para calcular o esforço interno:
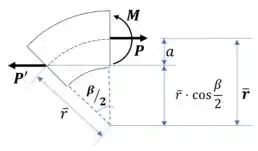
Pra calcular o momento, primeiro a gente precisa determinar o valor da distândia .
Com isso podemos calcular o sobre a viga:
Passo 3
Como a tensão gerada pela força é uma tração, então o ponto de maior tensão será na região de tração. O ponto de maior tração possível é o ponto .