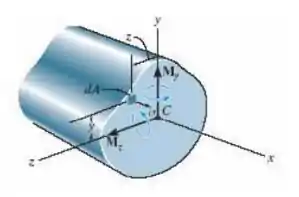
Considere o caso geral de uma viga prismática sujeita às componentes de momento fletor My
e Mz, como mostra a figura, quando os eixos x, y, z passam pelo centroide da seção transversal. Se o material for linear elástico, a tensão normal na viga é uma função linear da posição tal que σ = ax + by + cz. Usando as condições de equilíbrio: , , , determine as constantes a, b e c e mostre que a tensão normal pode ser determinada pela equação σ = [-(MzIy+MyIyz)y +(MyIz+MzIyz)z]/(IyIz-Iyz²).
Passo 1
Faaaala, meu povo bonito!! Tudo bem com vocês?? A nossa questão de hoje nos diz que essa viga, se o material dela for elástico, vai ter uma tensão normal no modelo de uma função linear para qualquer posição. A partir disso, ele nos pede os coeficientes da função (a, b e c) e para mostrar que a tensão pode ficar igual aquele troço ali. Bom, vamos começar.
Passo 2
Na hora que aplicamos a componente do eixo x do nosso σ direto na integral, temos que:
Opa, podemos fazer isso para o My e o Mz!!
E também sabemos que:
Passo 3
Como podemos cancelar alguns fatores com essa relação, vamos ter:
My = bIyz + cIy
Mz = -bIy - cIyz
Por causa dessas equações, chegamos a
a = 0, b = , c =
E, finalmente, podemos substituir esses coeficientes naquele nosso σ lá de cima que ele deu e achar
σ = y + z
Resposta
a = 0, b = , c =
σ = y + z