Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 78a
Uma viga de seção transversal mostrada é feita de um aço que é considerado ser elastoplásticos, com E=200GPa e . Por flexão em torno do eixo , determinar o momento fletor e o raio de curvatura, para que: (a) ocorra o início do escoamento; (b) as zonas plásticas, superior e inferior, da viga tenham 20 mm de espessura.
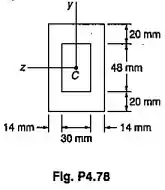
Passo 1
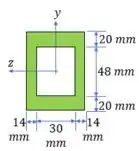
Como quase todas as questões de flexão, vamos começar calculando as propriedades geométricas:
Passo 2
A questão pede o momento fletor no início do escoamento. Em outras palavras, ela quer o maior momento elático permitido na viga
Passo 3
Prontinho! Agora é só calcular o raio de curvatura. Como o regime ainda é elástico, a gente pode usar a seguinte equação:
Resposta
Exercícios de Livros Relacionados
Um momento M deve ser aplicado a uma viga de seção transversal retangular, que é serrado de um tarugo de seção transversal circular. Determinar o raio d / b , para que:A máxima tensão σ m seja a menor
uma prancha de 38 m mx290m m pode ser reforçada pregando-se firmemente dois blocos de 38 m mx38 m m , como mostrado. Sabendo-se que σ A D M = 9,3M P a e G = 12G P a , determinar o maior momento que po
Um tubo de parede grossa é encurvado, em torno de um eixo horizontal, por um momento M . O tubo pode ser projetado com ou sem as quatro aletas. Pede-se:Usando uma tensão admissível de 140M P a , deter
Uma torção de uma barra quadrada é removida por fresagem, tal como é mostrado. A barra é então encurvada em torno de eixo horizontal diagonal por um momento M . Considerando o caso onde h = 0,9 h 0 ,
para a barra e o carregamento do exemplo 4.1, determinar:P raio de curvatura ρ ; O raio de curvatura ρ ' num plano transversal;O ângulo entre os lados originalmente verticais da barra. Usar E = 200G P