Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 27
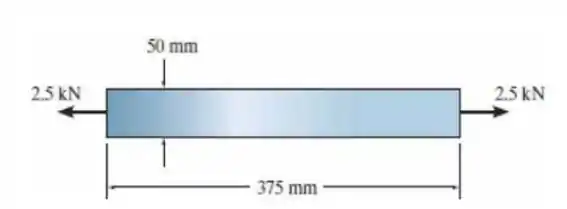
A barra de aço está sujeita à carga de tração de 2,5 kN. Se tiver 12 mm de espessura, determine a deformação por cisalhamento máxima absoluta. e
Passo 1
Fala galera, bora pra mais um problema. Primeiro, vamos determinar a tensão normal atuante:
Determinando-se a deformação no eixo longitudinal da peça e utilizando o coeficiente dado, teremos a deformação no outro eixo. Logo:
Logo, substituindo temos:
Portanto, a deformação no outro eixo, será:
Dadas as deformações nos eixos, podemos obter a deformação média, que será a média das duas deformações calculadas:
Passo 2
Com isso, vamos calcular o raio do círculo de Mohr, para que possamos determinar as deformações principais:
Logo, teremos:
Com isso, podemos obter o dado pedido pelo problema:
Resposta
Exercícios de Livros Relacionados
Determine os planos principais e as tensões principais para o estado plano de tensões que resulta da superposição dos dois estados planos mostrados.
Para o estado de tensões mostrado, determine a tensão de cisalhamento máxima quando (a) σ z = + 4k s i , (b) σ z = - 4k s i , (c) σ z = 0 .
Para o estado de tensão mostrado na figura, determine o valor de τ x y para o qual a tensão de cisalhamento máxima é (a) 60 MPa, (b) 78 MPa.
O estado plano de tensões mostrado ocorre em um componente de máquina feito de aço com σ E = 206,9M P a . Utilizando o critério da máxima energia de distorção, determine se o escoamento ocorrerá quand
Resolva os Problemas 7.5 e 7.9 usando o círculo de Mohr