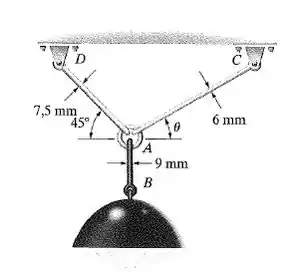
A luminária de 250 N é sustentada por três hastes de aço interligadas por um anel em A. Determine qual das hastes está submetida à maior tensão normal média e calcule seu valor. Considere θ = 45°. O diâmetro de cada haste é dado na figura.
Passo 1
Fala aí galerinha do responde aí, bora pra outra questão.
Sabemos que a tensão é dada pela força dividida pela área, certo? Assim, temos que calcular a força em cada haste e dividir pelas respectivas áreas, e vê qual dá o valor maior. Já que ele quer a maior tensão, beleza?
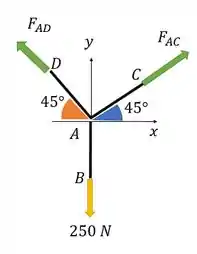
O DCL fica:
Passo 2
Aí decompondo as forças e usando as equações de equilíbrio, para achar as forças:
Note que temos 2 equações e 2 incógnitas, logo, podemos fazer um sistema. Resolvendo o sistema, teremos:
E já sabemos que
Passo 3
Já temos as forças que atuam nas hastes. Basta agora calcular as áreas:
Com as forças e as áreas, podemos calcular as tensões nas hastes:
Podemos ver que a haste AC possui a maior tensão.
Resposta
A haste AC possui a maior tensão, que é de