Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 46

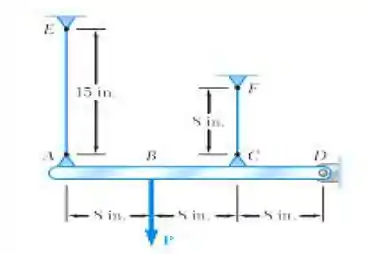
A barra rígida AD é suportada por dois cabos de aço com 1/16 in. de diâmetro ( E = 29   x   10 6   p s i ) e por um pino e um suporte em D. Sabendo que os cabos foram inicialmente tensionados, determine (a) a tração adicional em cada cabo quando uma ação de 120 lb é aplicada em B, (b) a correspondente deflexão do ponto B.

Passo 1

Fala aí gurizada tudo belezinha?????? Antes de determinarmos a tensão e o deslocamento pedidos pelo exercício, vamos então desenhar o diagrama corpo livre, vem comigo :D

Seja θ a rotação da barra ABCD.

Então:

δ A = 24 θ               δ C = 8 θ

δ A = P A E L A E A E

Isolando P A E temos: P A E = E A δ A L A E = 29   x   10 6   x   π 4   x   1 16 2 x   ( 24 θ ) 15 = 142,353   x   10 3 θ

δ C = P C F L C F A E

Isolando P C F temos: P C F = E A δ C L C F = 29   x   10 6   x   π 4   x   1 16 2 x   ( 8 θ ) 8 = 88,971   x   10 3 θ

Passo 2

Desenhando o diagrama de corpo livre ABCD

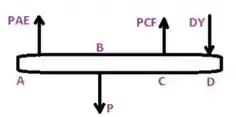
Agora partiu calcular o somatório do momento em D....

+ ∑ M D = F x d = 0

- 24 P + 16 P - 8 P C F = 0

Substituindo os valores obtidos no passo 1 temos.............

- 24   x   142,353   x   10 3 θ + 16   x   120 -   8   x   88,971   x   10 3 θ = 0

θ = 0,46510   x   10 3 r a d  

Agora sim podemos calcular tração adicional e a deformação :D

  1. P A E = 142,353   x   10 3   x   0,46510   x   10 - 3 P C F = 88,971   x   10 3   x   ( 0,46510   X   10 - 3 )
  2. δ B = 16 θ = 16   x   ( 0,46510   x   10 - 3 )

Resposta

  1. P A E = 66,2   l b P C F = 41,4   l b
  2. δ B = 7,44   x   10 - 3 i n . ↓
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio de nylon está submetido à forca de tração de 8,5 N. Sabendo que E=3,3G P a e que o comprimento do fio é incrementado em 1,1%, determine (a) o diâmetro do fio, (b) a tensão do fio.
Uma barra de controle feita de latão não deve se alongar mais de 3,0 mm quando a tração no fio for 4 kN. Sabendo que E=105G P a e que a máxima tensão normal admissível é 180 MPa, determine (a) o menor
Um tubo de ferro fundido é utilizado para suportar uma força de compressão. Sabendo que E = 10x10 6 p s i e que a máxima variação admissível no comprimento é 0,025%. Determine (a) a tensão normal máxi
Uma ação axial de intensidade P = 15 kips é aplicada à extremidade C da haste ABC. Sabendo que E = 29x10 6p s i , determine d da porção BC para que a deflexão do ponto C seja de 0,05 in.
Um fio de nylon esta submetido a uma tração de 10 N. sabendo que E = 3,2G P a , que a máxima tensão de tração admissível é de 40 MPa e que o comprimento do fio não pode ser incrementado em mais do que