Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 114

Resolva o Problema 2.113 sabendo que a = 1,76   m e que a intensidade da força Q aplicada em B é aumentada gradualmente de zero até 135   k N .

Passo 1

E ai gurizada tudo belezinha? Espero que sim !! O enunciado pede que a gente determine valor da tensão normal em cada barra elástica , antes demais nada vamos desenhar o diagrama de corpo livre , vem comigo :D

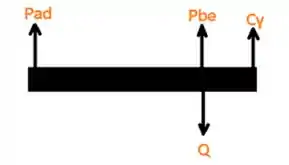
Agora podemos determinar o somatório do momento em C, partiu determinar :D

∑ M C = 0 :       1,76   x   Q - P B E - 2,64   P A D = 0

Deformação: δ A = 2,64 θ ,         δ B = a θ - 1,76 θ

Análise estática:

A = 37,5   x   6 = 225   m m 2 = 225   x   10 - 6 m 2

P A D = E A L A D δ A = 200   x   10 9   x   225   x   10 - 6 1,7 δ A = 26,47   x   10 6 δ A = 26,47   x   10 6   x   2,64 θ = 69,88   x   10 6 θ

Calma galera que falta pouco, precisamos determinar as relações de tensão e força

σ A D = P A D A = 310,6   x   10 9 θ P B E =   E A L B E δ B = 200   x   10 9   x   225   x   10 - 6 1,0 δ B = 45   x   10 6 δ B = 45   x   10 6   x   1,76 θ = 79,2     x   10 6 θ   σ B E = P B E A = 352   x   10 9 θ

Passo 2

Considerando

Q = P B E + 2,64 1,76 P A D = P B E + 1,500 P A D = 73,8   x   10 6 + 1,500   x   69,88   x   10 6 θ = 178,62   x     10 6 θ

θ Y para a ligação BE:

σ B E = σ Y = 250   x   10 6 =   352   x   10 9 θ θ Y = 710,23   x     10 - 6 Q Y = 178,62   x     10 6   x   710,23   x     10 - 6 = 126,86   x   10 3 N  

  1. Desde a Q = 135   x   10 3 > Q Y , ligação BE temos:

    2. P B E = A σ Y = 225   x   10 - 6   x   250   x   10 - 6 = 56,25   x   10 3 N  

    P A D = 1 1,500 x   ( Q - P B E ) = 52,5   x   10 3 N     σ A D = P A D A = 52,5   x   10 3 225   x   10 - 6 = 233,3   x   10 6

    Da análise estática de AD temos

    θ = P A D 69,88   x     10 6 = 751,29   x   10 - 3 r a d

  2. δ B = 1,76 θ = 1,322   x   10 - 3 m  

Resposta

  1. σ B E = σ Y = 250   M P a

    2. σ A D = 233   M P a

  2. δ B = 1,322   m m   ↓
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada cabo tem uma área de seção transversal igual 100 mm² e é feito de um material elastoplástico para o qual σ E = 345M P aeE = 200G P a . Uma força Q é aplicada na barra rígida ABC através do ponto
Resolva o Problema 2.109 supondo que os cabos foram substituídos por barras com a mesma área de seção transversal e o mesmo material. Supondo ainda que as barras foram fixadas de modo que possam supor
Resolva o Problema 2.113 supondo que a intensidade da força Q aplicada em B seja aumentada gradualmente de zero até 260k N e depois diminuída de volta para zero. Sabendo que a = 0,640m , determine (a)
Para a barra composta do Problema 2.111, se P é gradualmente aumentada desde zero até 436k N e depois diminuída até zero, determine (a) a deformação máxima da barra, (b) a tensão máxima nas barras de
Para a barra composta do Problema 2.107, se P é aumentada gradualmente desde zero até que o deslocamento do ponto C atinja um valor máximo de δ m = 0,3m m e depois diminuída novamente até zero, determ