Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas de Revisão - Ex. 59
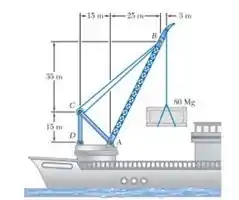
No guindaste marítimo mostrado, sabe-se que a barra de conexão CD tem seção transversal constante de 50 X 150 mm. Para o carregamento mostrado, determine a tensão normal na porção central da barra de conexão.
Passo 1
Fala ai gurizada tudo belezinha? Para facilitar todos os cálculos, vamos primeiramente desenhar o diagrama de corpo livre, partiu???
Antes de mais nada Peso do carregamento:
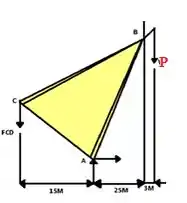
Então partiu calcular o diagrama do corpo livre...
Ufaaaaaaaa , agora sim podemos calcular a tensão:
+195,3 X Pa
Resposta
= +195,3 MPa
Exercícios de Livros Relacionados
Expressando por ε a “deformação técnica” em uma amostra tracionada, mostre que a determinação exata é ε t = ln 1 + ε .
O volume de uma amostra tracionada é essencialmente constante, enquanto a derformação plástica ocorre. Se o diâmetro inicial da amostra é d 1 , mostre que quando o diâmetro é d 2 a deformação é ε t =
Determinar a deflexão do cume A de um paraboloide de revolução homogêneo, de altura h , densidade ρ e módulo de elasticidade E , devido ao seu próprio peso.
Determinar a deflexão do cume A de um cone circular homogêneo, de altura h , densidade ρ e módulo de elasticidade E , devido ao seu próprio peso.
Uma amostra para ensaio de 5m m de espessura deve ser cortada de uma placa de vinil ( E = 3,10G P a ) , e submetida a uma carga de tração de 1,5k N . Determinar ( a ) a deformação total da amostra; (