Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas de Revisão - Ex. 64
Sabendo que a barra de conexão DE tem 1/8 in de espessura e 1 in de largura, determine a tensão normal na porção centra dessa barra quando (a)
Passo 1
Fala aí galera tudo bemm??? Primeiramente vamos desenhar o diagrama de corpo livre para facilitar os cálculos :D
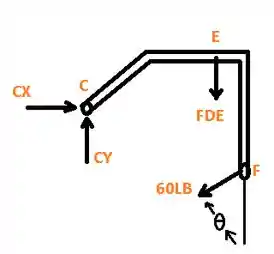
Agora devemos calcular a área para este trecho do diagrama
Então temos:
Passo 2
Calculando as tensões para os ângulos, dados temos:
- = -80lb
- = 90°: = -40lb
Resposta
- = −640psi
- = -320psi
Exercícios de Livros Relacionados
Para a barra e o suporte do Prob 2.18, determinar a maior carga P admissível, se a deflexão nos pontos A e B não devem exceder a 0,108m m e 0,305m m , respectivamente.
Cada uma das hastes de ligação AB e CD; são de aço( E = 200 G P a ) e tem seção transversal uniforme de 6,4 × 25,4m m . Determinar a maior carga que pode ser aplicada ao ponto E , sendo que a deflexão
Um tubo cilíndrico de poliestireno de parede fina E = 3,1G P a , com 3,2m m de espessura e uma placa rígida circular (é ostrada apenas parte dela), são usadas para suportar uma barra de aço A B ( E =
Para a barra composta do Prob 2.9, determinar a maior carga P admissível se a deformação total da barra não deve exceder a 1mm e a tensão normal ser no máximo igual a 180 Mpa
Para a barra composta do Prob 2.10, determinar a maior carga P admissível se em valores absolutos a deformação total da barra e sua máxima tensão normal não podem exceder a 0,2 m m e 75 M P a , respec