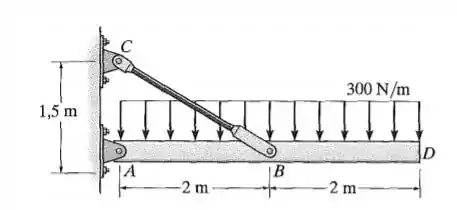
A barra rígida é sustentada pela haste acoplada por pino, com área de seção transversal de e feita de alumínio . Determine a deflexão vertical da barra em quando a carga distribuída for aplicada.

Vamos aplicar a equação de equilíbrio de momentos em relação ao ponto da nossa figura para achar o valor de , a força em , que vai servir para a gente achar o alongamento na haste.

Primeiramente devemos observar que a força na haste pode ser decomposta em duas componentes onde, para nosso caso, só nos interessa a componente vertical que é a única que gera momento:

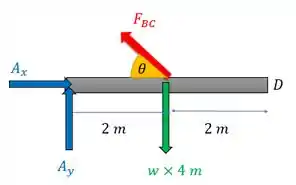
Se chamarmos o ângulo destacado na imagem de , nossa componente vertical da força pode ser descrita por . Além disso, devemos lembrar que o carregamento pode ser concentrado no centro da barra com módulo e

Das reações de suporte vamos ter adotando o sentido anti-horário como positivo

Podemos achar esse seno pela geometria da figura. Percebe que tem um triangulo retângulo nela:

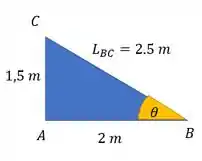
Vemos que tem porque esse é um triângulo do tipo 3/4/5, mas se não ficar claro de cara, cê sempre pode fazer pitagoras e achar o lado que falta. Aí desse triângulo a gente tem que

Substituindo na nossa expressão do equilíbrio

Isolando a força:

Aí com essa força a gente consegue achar o alongamento em :

Substituindo os valores:

Depois da deformação de , o triângulo que a gente viu antes vai ficar assim:

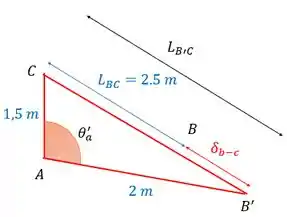
Dado que o ponto sofre uma deflexão podemos definir um novo ponto no qual o nosso ponto se localiza agora. Dessa forma, se traçarmos um triângulo com os pontos podemos estabeler o seguinte

Como a barra é rígida, a distância entre não muda, logo, também vale .

Através da lei dos cossenos também podemos fazer

Pela figura, a gente pode achar o ângulo que a barra rígida inclinou em relação a posição horizontal:

Então, finalmente, podemos achar a aproximação de arco para achar a deslocamento vertical de , já que esse ângulo de rotação do segmento é bem pequeno:

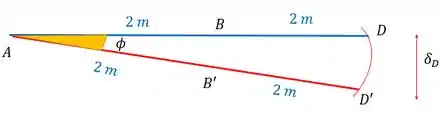
Aí vai ser o comprimento do arco de raio , assim: