Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 6
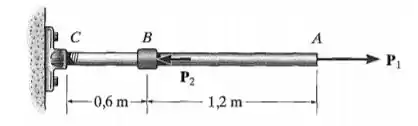
O conjunto é composto por uma haste de aço e uma haste de alumínio , cada uma com diâmetro de . Determine as cargas aplicadas se se deslocar para a direita e se deslocar para a esquerda quando as cargas forem aplicadas. O comprimento de cada segmento quando não alongado é mostrado na figura. Despreze o tamanho das conexões em e e considere que elas são rígidas.
Passo 1
Fala!
Como os materiais tratados no problema são o aço e o Alumínio temos o módulo de elasticidade tabelado e dado por .
Queremos encontrar e . Como ele dá os deslocamentos, temos uma dica que de que vamos usar:
Onde é a extensão do segmento que estamos analisando.
Vamos então refletir em como podemos usar essa bonita. Bora!
Passo 2
Vamos olha para AB. Temos que deslocou para a direita. Mas a sua outra extremidade deslocou para a esquerda. Então ela sofreu tração, com um alongamento total de .
Que força causou essa tração? Se a gente cortar a barra na essa seção e olhar para a direita, olha o que acontece:
Vemos que a carga interna nessa barra, é igual ao , pelo equilíbrio. Então a gente pode usar a fórmulinha para escrever:
Passo 3
Agora para . A extremidade C não se mexeu porque ela está no engaste. Mas a extremidade B se mexeu para esquerda. Ou seja, esse pedaço sofreu compressão. E seu encolhimento foi de .
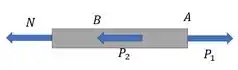
Vamos achar o esforço interno desse pedaço, fazendo uma seção nesse intervalo .
Pelo equilíbrio de forças na horizontal:
Assim, podemos escrever, usando a fórmulinha: