Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 14
Um suporte para tudos apoiado por molas é composto por duas molas que, na posição original, não estão alongadas e têm rigidez , três hastes de aço inoxidável com diâmetro de com diâmetro de , e uma viga rígida . Se o tubo for deslocado quando estiver cheio de fluido, determine o peso do fluido.
Passo 1
Falaaa! Tá bem?
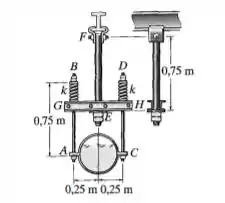
Não se assusta com o desenho, tá? Temos um tubo, segurado por duas hastes. E essas duas, seguradas por uma haste só EF, e essa ligação acontece através do corpo rígido GH. Esse desenho do lado é só uma visão de outro ângulo da haste EF.
A gente quer encontrar o peso do nosso fluido dado o deslocamento total do tubo quando cheio de fluido.
Como o tubo é suportado por esse sistema de hastes verticais, o deslocamento total dele é resultado do alongamento dessas hastes quando submetidas a carga peso do fluído.
Precisamos lembrar, então, que o deslocamento devido alongamento em cada haste é dado por
Como essa expressão relaciona alongamento e carga aplicada, é através dela que a gente chega no peso do fluído. Vamos montá-la para cada hastezinha que a gente tem.
Além disso, precisamos saber que para o aço inoxidável o módulo de elasticidade é tabelado e dado por .
Vamos seguir!
Passo 2
Queremos descobrir para cada haste que a gente tem.
Vamos olhar só para as hastes diretamente ligadas ao tubo:
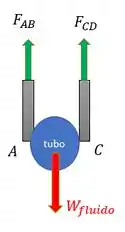
Por simetria, cada uma vai suportar metade do peso do fluído, então
E haste
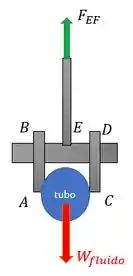
Por equilíbrio, a força normal interna nela é
Passo 3
Como estamos tratando de áreas de circunferências, elas serão dadas por
Agora vamos entender a situação. O deslocamento do tubo vai ser influenciado diretamente pelo deslocamento em EF. Se o ponto E desce, o tubo também. Vamos calcular então.
Aplicando a fórmula descrita no primeira passo vamos ter
Passo 4
Agora vamos olhar para o ponto . Se ele desce, nosso tubo também desce. (pela simetria, ocorre o mesmo com B). Ele desce porque desce, mas também por causa do comportamento da mola.
Talvez essa mola na figura tenha te assutado.
Mas relaxa. Ela está incialmente sem deformação. Quando a força é aplicada na haste CD, o ponto D desce porque a força o puxa para baixo. E com isso, a mola é emprensada entre esse ponto e a haste rígida GH, causando uma deformação nela de .
Essa deformação causada na mola é exatamente o valor que o ponto vai descer em relação ao ponto , porque é a variação de comprimento entre a mola no ínicio e no final. Podemos encontrar esse valor pela fórmulinha:
Com isso podemos encontrar que o deslocamento do ponto é dado pela soma entre o deslocamento de e a deformação da mola:
Passo 5
Belezinha. Olhamos o ponto . Agora queremos o deslocamento do ponto , que está alinhado ao tubo. O deslocamento dele vai ser o que a gente achou para mais o próprio alongamento de CD, dado por
Da simetria do problema teremos . E temos que o ponto está ainhado ao tubo, então o deslocamento de é o deslocamento total do tubo. Sendo assim, nosso deslocamento total do tubo tem essa expressão:
Passo 6
O enunciado diz que isso é igual a . Substituindo e isolando :