Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 103
A viga é suportada pelos três postes , e de comprimentos iguais. Os postes e têm diâmetro de e são feitos de alumínio, para o qual e . O poste tem diâmetro de e é feito de latão, para o qual e . Determine o menor valor de de modo que somente as hastes e sofram escoamento e todos os postes sofram escoamento.
Passo 1
Três postes apoiam uma viga rígida. Dois carregamentos são aplicados
Características dos postes e :
- Alumínio: , .
- Área transversal: .
- Latão: , .
- Área transversal: .
Características do poste :
Queremos o menor valor que precisa assumir para ocorrer:
- Caso : carregamentos fazem com que apenas os postes e escoem.
- Caso : carregamentos fazem com que todos os postes escoem.
Beleza, pra verificarmos cada caso, vamos precisar das tensões , e em cada caso. Fórmula da tensão:
Como sabemos as áreas, nos falta achar as forças!
Passo 2
Diagrama de corpo livre.
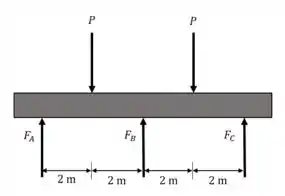
Equilíbrio de momentos ao redor de :
Beleza, é o que esperávamos mesmo por causa da simetria. Pra facilitar, vamos usar e .
Agora vejamos o equilíbrio de forças:
Essa condição é verdade pros dois casos ( é conhecido!). Vamos caçar mais relações. Vejamos a condição de compatibilidade.
Passo 3
O peso vai comprimir os postes, diminuindo o tamanho deles. O poste de latão e os postes de alumínio vão ter que diminuir o mesmo comprimento!
Primeiro estamos procurando para a situação limite em que os postes começam a sofrer escoamento. O menor valor que precisa no Caso vai ocorrer no regime elástico. Ótimo! Podemos usar a relação carga-deslocamento:
Substitua os valores. Como vamos tratar do Caso primeiro, procure deixar em função de .
Atenção que só podemos usar essa fórmula enquanto estamos no regime elástico!
Passo 4
Substitua na condição de equilíbrio, aí teremos uma expressão pro carregamento na situação de regime elástico!
Para o Caso ocorrer, precisamos que a tensão nos postes de alumínio seja exatamente . Pela fórmula da tensão, isso nos dá:
O que corresponde a carregamentos para o Caso de
Passo 5
Beleza, calma que ainda falta um detalhe pro Caso ! Temos que conferir se é válido mesmo: se apenas os postes e escoaram.
Você tem que conferir isso usando necessariamente o equilíbrio de forças:
Agora que temos a força no poste de latão, verifique se ele ainda está no regime elástico:
Beleza, é menor que , como queríamos.
Caso acabou. Precisaríamos de um carregamento de .
Vejamos o Caso !
Passo 6
O Caso pede que achemos o carregamento que faz todos os postes escoarem! Agora precisamos pensar bastante.
Nós sabemos que no limite para começar a escoar, os postes e desenvolvem forças de . Isso aí acontece quando a tensão nesses postes é especificamente .
Para o poste escoar, com certeza vamos precisar de um carregamento maior que . A questão deveria ter nos dito o que acontece com e para carregamentos mais altos (um gráfico tensão-deformação, por exemplo)...
Como não temos essa informação, vamos assumir que os postes são elastoplásticos! Então a tensão em e permanece sendo e a força nesses postes será
Progresso! Vamos ver como fica a força no poste de latão para o caso .
Passo 7
Para achar , usamos a mesma lógica do Passo 4. Queremos que a tensão em seja exatamente !
Passo 8
Show, temos todas as forças! Agora é só calcular o carregamento pelo equilíbrio de forças para o Caso . Usando e ,
Fechou!!
OBS: você não pode usar de jeito nenhum no Caso hein! No Caso , os postes e não estão mais no regime elástico. Fique atento!
Resposta
Menor valor de para que somente os postes e escoem: .
Menor valor de para todos os postes escoem: .