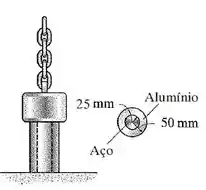
O peso de () é assentado lentamente no topo de um poste feito de alumínio com núcleo de aço . Se ambos os materiais puderem ser considerados elásticos perfeitamente plásticos, determine a tensão em cada um deles.
Passo 1
Fala!
Um peso de é sustentando por um poste feito de dois materiais: internamente de aço e externamente de alumínio. Os materiais devem ser considerados elastoplásticos.
Vamos anotar tudo, e fique atento: a questão fala sobre os materiais serem elastoplásticos, então precisamos checar escoamento!
Características do poste:
- Parte interna de Aço : , . (Tabelado)
- Parte externa de alumínio : , . (Tabelado)
- Área de aço: .
- Área de alumínio: .
Queremos saber a tensão ocorrendo em cada material!
Primeiro vamos supor que os materiais permanecem elásticos (tensões menores que a tensão de escoamento). Isso significa, nessa questão, em resolver um problema estaticamente indeterminado.
Aí vamos ver se alguma das tensões calculadas é maior que a tensão de escoamento! Se for, vamos tratar de usar o comportamento dos elastoplásticos. Vai ser tranquilo!
Passo 2
Para descobrir a tensão nos materiais, precisamos das forças neles.
Começamos com equilíbrio de forças. Só tem uma direção no problema, e o aço e o alumínio têm que sustentar o peso:
Show, vamos precisar de mais uma equação. Vejamos a condição de compatibilidade.
Passo 3
O peso vai comprimir o poste, reduzindo o tamanho dele. Tanto a parte de aço quanto a parte de alumínio têm que diminuir o mesmo comprimento!
Temos fórmula pra esses caras. Relação carga-deslocamento:
Atenção que só podemos usar essa fórmula agora porque estamos supondo regime elástico! Depois vamos verificar se estamos certos em usar isso.
Passo 4
Vamos resolver o sistema de equações para achar as forças. Substitua na equação que veio do equilíbrio:
Passo 5
Divida cada força pela área, assim temos as tensões:
Calma que não acabou! Temos que checar se estamos no regime elástico mesmo!!
A tensão no alumínio é menor que a tensão de escoamento dele, . Show!
Mas a tensão no aço está maior que a tensão de escoamento: ... Iiiiih, deu xabu!
Temos que pensar o problema de novo. Mas agora a gente sabe o seguinte: o aço com certeza vai escoar!
Passo 6
Como os materiais são elastoplásticos, quando eles atingem a , a tensão que eles suportam não vai aumentar mais. Ele só continuam deformando indefinidamente. Cê pode ver isso no gráfico de deformação de um material elastoplástico:
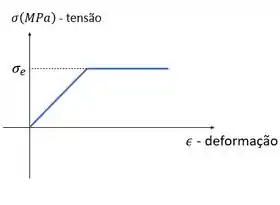
Assim, a tensão neles vai continuar sendo a tensão de escoamento! Então a tensão no aço é na verdade:
Beleza, pro aço acabou!! Agora vamos ver pro alumínio!
Se o aço está sob tensão , podemos multiplicar pela área pra saber qual é o máximo de carregamento que ele está aguentando:
Aí a gente volta pra equação de equilíbrio:
Atenção: você tem que fazer essa conta com a condição de equilíbrio! A relação que achamos pela compatibilidade só seria válida se os dois materiais estivessem em regime elástico, mas eles não estão. Cuidado com isso!
Passo 7
Está quase lá, vamos ver a tensão no alumínio:
Não esqueça de conferir se essa tensão ultrapassou o limite de escoamento .
Como , então está tudo certo e acabou! Se por acaso tivesse dado maior, significaria que o alumínio também escoou e que o poste não conseguiu suportar o peso!
Ufa! Terminamos!
Resposta
Tensão na parte de aço: .
Tensão na parte de alumínio: .