Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 71
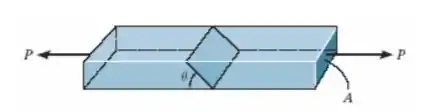
A barra tem área de seção transversal e está submetida à carga axial . Detetmine a tensão normal média e a tensão de cisalhamento média que agem na seção sombreada que está orientada a um ângulo em relação à horizontal. Represente em gráfico a variação dessas tensões em função de .
Passo 1
Precisamos saber quais são as forças que atuam nesse nosso sistema para que então consigamos descobrir quais os valores de tensões normal e de cisalhamento que são dadas por
Com
P: resultante da força normal;
A: Área da seção transversal;
F: Força cortante total;
Área cortante;
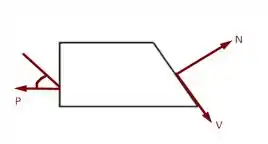
Para sabermos quais forças são essas que atuam no nosso sistema façamos o seguinte diagrama de forças
Passo 2
Pela figura vemos que é possível decompor a força de tal forma que ela se adeque as direções de e de , assim teremos
Sendo que e se referem ao sistema de coordenadas cartesianas deslocado de um ângulo . Dessa forma, podemos fazer as equações de equilíbrio pra esse novo sistema de coordenadas, assim teremos
Para esse caso também teremos a Área da seção transversal deslocada assim temos
Passo 3
Agora, temos tudo para calcular as tensões desejadas pela questão, basta substituirmos os dados e assim iremos obter
Para a tensão de cisalhamento vamos ter
Podemos, ainda, plotar um esboço dos gráficos dessas funções e vamos obter
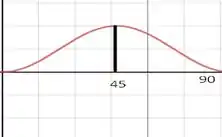
Para o gráfico da tensão de cisalhamento onde temos seu valor de pico em . Já para a tensão normal vamos ter o seguinte esboço
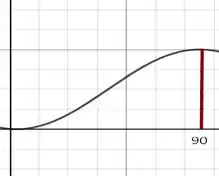
Onde nossa função tem seu ápice em .