Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 127

Para a barra uniforme com o carregamento mostrado e usando o teorema de Castigliano, determinar a deflexão no ponto B

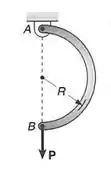
Passo 1

Primeiramente devemos determinar o momento na curva

+ ↺ Σ M J = 0     M - P a - Q b = 0

M = P a + Q b = P R s i n Q + Q R 1 - c o s Q

2 M 2 P = R s i n Q     2 M 2 Q = R 1 - c o s Q                   S e t   Q = 0

Passo 2

Considere para determinar a deflexão os dados abaixo :D

δ b = δ U 2 Q = 1 E I ∫ 0 π 2 M 2 M 2 Q R d Q = 1 E I ∫ 0 π 2 P R   S i n Q R 1 - c o s Q R d Q

= P R 3 E I ∫ 0 π 2 s i n Q - s i n Q c o s Q d Q = P R 3 E I ( - c o s Q - 1 2 sin 2 ⁡ Q ) 0 π 2

= P R 3 E I - cos ⁡ π 2 + cos ⁡ 0 - 1 2 sin 2 ⁡ π 2 + 1 2 sin 2 ⁡ 0

= P R 3 E I 0 + 1 - 1 2 + 0 = 1 2 P R 3 E I

Resposta

1 2 P R 3 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o prob. 11.50 assumindo que o tubo seja substituído por uma barra maciça de alumínio com as mesmas dimensões externas que as do tubo.
O bloco D de 2 kg cai da posição mostrada sobre a extremidade de uma barra de 16mm de diâmetro. Sabendo que E = 200 GPa, determine (a) a deflexão máxima na extremidade A, (b) o momento fletor máximo n
11.53 O bloco D de 10kg é solto desde uma altura h = 450 mm sobre uma viga de alumínio AB. Sabendo que E = 70 GPa, determine (a) a máxima deflexão do ponto E, (b) a máxima tensão na viga.
O bloco D de 2kg cai da posição mostrada sobre a extremidade de uma barra de 16mm de diâmetro. Sabendo que E = 200 GPa, determine (a) a deflexão máxima na extremidade A, (b) o momento fletor máximo na
Um mergulhador de peso igual a 711,7 N salta de uma altura de 508mm na extremidade C de um trampolim cuja seção transversal é a mostrada. Considerando que as pernas do mergulhador permanecem rígidas e