Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 54

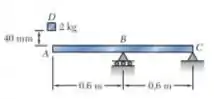
O bloco D de 2kg cai da posição mostrada sobre a extremidade de uma barra de 16mm de diâmetro. Sabendo que E = 200 GPa, determine (a) a deflexão máxima na extremidade A, (b) o momento fletor máximo na barra e (c) a tensão normal máxima na barra.

Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:

Use o Apêndice D.

y 2 = P m L 3 3 E I         y 1 = L θ B = P m L 3 3 E I

y m = y 1 + y 2 = 2 P m L 3 3 E I     y m = 2 P m L 3 3 E I

U m = 1 2 P m y m = 1 2 3 E I 2 L 3 y m = 3 E I 4 L 3 y ² m

W h + y m = U m

W h + y m = 3 E I 4 L 3 y ² m

Passo 2

Substitua os dados fornecidos:

4   l b 1,5   i n . + y m = 3 29 × 1 0 6 p s i 7,49 × 1 0 - 3 i n 4 4 ( 24   i n . ) ³   y ² m

(a)

6 + 4 y m = 11,784 y ² m

Resolva quadrática:

y m = 0,9032   i n .                     y m = 0,903   i n .

(b)

P m = 3 E I 2 L 3 y m = 3 29 × 1 0 6 p s i 7,49 × 1 0 - 3 m 4 2 24   i n . 3 0,9032   i n . = 21,29   l b

M m = M E = P m L = 21,29   l b 24 i n . = 510,96   l b ∙ i n .

M m = 511   l b ∙ i n .

Passo 3

(c)

σ m = M m c I = M m S = 510,96   l b ∙ i n . 23,97 × 1 0 - 3 i n 3

σ m = 21,3   k s i

Resposta

Então gurizada, como acabamos de calcular, temos a resposta de (a) y m = 0,903   i n . ; (b) M m = 511   l b ∙ i n . ; (c) σ m = 21,3   k s i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo de alumínio com a seção transversal mostrada é atingido diretamente na sua seção média por um bloco de 6kg movendo-se na horizontal com uma velocidade de 2m/s. Utilizando E = 70 GPa, determine
Resolva o prob. 11.50 assumindo que o tubo seja substituído por uma barra maciça de alumínio com as mesmas dimensões externas que as do tubo.
O bloco D de 2 kg cai da posição mostrada sobre a extremidade de uma barra de 16mm de diâmetro. Sabendo que E = 200 GPa, determine (a) a deflexão máxima na extremidade A, (b) o momento fletor máximo n
11.53 O bloco D de 10kg é solto desde uma altura h = 450 mm sobre uma viga de alumínio AB. Sabendo que E = 70 GPa, determine (a) a máxima deflexão do ponto E, (b) a máxima tensão na viga.