Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 93

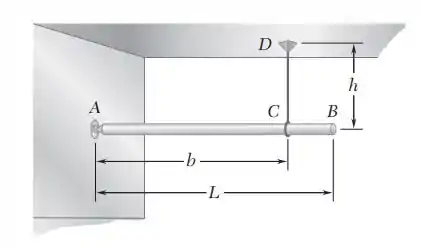
Uma barra uniforme de comprimento L é suportada por um suporte esférico em A e por um fio vertical CD. Deduza uma expressão para o período de oscilação da barra se a extremidade B recebe um pequeno deslocamento no plano horizontal e então é liberado.

Passo 1

E ai gurizada tudo belezinha??? O enunciado pede que a gente deduza uma expressão para o período de oscilação da barra se a extremidade B recebe um pequeno deslocamento no plano horizontal e então é liberado.

Passo 2

Consideramos primeiramente a posição 1 :D

Posição ① (Defleção Máxima)

Olhando de cima:

Deslocamento horizontal de C:

x C = b θ m

Olhando da Direita:

Ø m = x c h = b h θ m

y c = h 1 - C o s   Ø m ≈ 1 2   h Ø m 2

y c = 1 2 h b h θ m 2 = 1 2 b ² h θ m 2

ȳ m = y G = A G A G - y c = 1 2   L b 1 2 ∙ b 2 h   θ m 2

ȳ m = 1 4 ∙ b L h θ m 2

Temos, T 1 = 0

V 1 = m g b m = 1 4 m g b L h   θ m 2

Passo 3

Consideramos primeiramente a posição 2 :D

Posição ②(Defleção Máxima)

Olhando de cima:

T 2 = 1 2   Ī   θ m 2 ˙ + 1 2   m ῡ m 2 = 1 2 1 12   m L ²   θ m 2 ˙ + 1 2   m L 2   θ ˙ ²

T 2 = 1 6   m L 2   θ m 2 ˙    

V 2 = 0

Passo 4

Conservação de energia: T 1 + V 1 = T 2 + V 2 :

0 + 1 4 m g b L h   θ m 2 ˙ = 1 6   m l 2   θ m 2 ˙  

Mas para movimentos harmônicos simples,

θ m ˙ = ω n θ m

1 4 m g b L h θ m 2 = 1 6   m L 2 ( ω n θ m ) ²

ω n 2 = 3 2 b g h L

Período de vibração: τ n = 2   π ω n

Resposta

τ n = 2 π 2   h L 3   b g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.53. O braço ACB gira em torno do ponto C com velocidade angular de 40 rad /s no sentido anti-horário. Dois discos de atrito A e B estão presos por pinos em seus centros ao braço ACB do modo mostrad
15.55. Sabendo que a manivela AB tem uma velocidade angular constante de 160 rpm no sentido anti-horário, determine a velocidade angular da barra BD e a velocidade do colar D quando (a) 0, (b) 90°.
15.57. No sistema biela-manivela de motor mostrado na figura, l 160 mm e b 60 mm. Sabendo que a manivela AB gira com uma velocidade angular constante de 1.000 rpm no sentido horário, determine a veloc
15.56. Sabendo que a manivela AB tem uma velocidade angular constante de 160 rpm no sentido anti-horário, determine a velocidade angular da barra BD e a velocidade do colar D quando (a) 60°.
15.61. Uma cremalheira reta repousa sobre uma engrenagem de raio r 60 mm e está presa ao bloco B como mostra a figura. Sabendo que nesse instante a velocidade do bloco B é de 200 mm/s para a direita e