Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 56

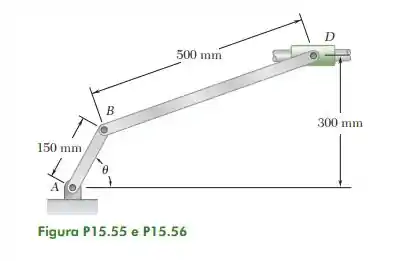
15.56. Sabendo que a manivela AB tem uma velocidade angular constante de 160 rpm no sentido anti-horário, determine a velocidade angular da barra BD e a velocidade do colar D quando (a) 60°.

Passo 1

Vamos matar mais uma?

O enunciado nos dá

ω A B = 160   r p m = 16,75 r a d s

Então podemos calcular

v B = r A B ⋅ ω A B

Então

v B = 150 ⋅ 16,75 = 2513,27 m m s

Com essas informações a gente pode continuar o exercício.

Passo 2

No item (a) temos θ = 0 , então toda velocidade em B vai ser uma velocidade pra cima no sentido horizontal.

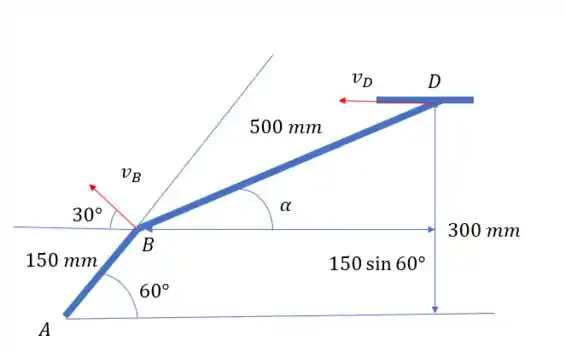
A velocidade v B é perpendicular a AB e sabemos que uma linha reta forma um ângulo de 180 ° , com essas informações podemos deduzir que a velocidade v B tem um ângulo de 30 ° com o eixo x negativo.

Pela imagem podemos ver também que

sin ⁡ α = 300 - 150 sin ⁡ 60 ° 500 = 19,89 °

Então temos os vetores:

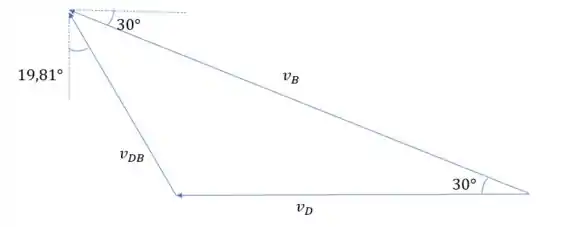
Sabendo que um ângulo reto tem 90° e que os ângulos internos de um triangulo tem 180° podemos fazer

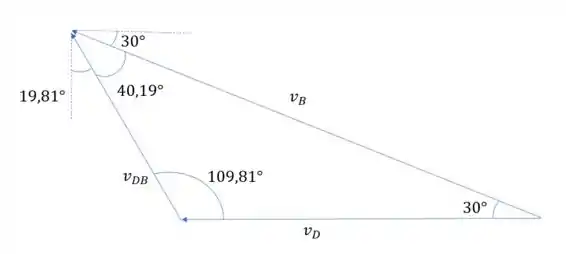
Passo 3

Podemos usar a lei dos senos para fazer

v D sin ⁡ 40,11 ° = v D B sin ⁡ 30 ° = v B sin ⁡ 109,89 °

Ou seja

v D = v B sin ⁡ 40,11 ° sin ⁡ 109,89 °  

Mas

v B = 2513,27   m m s

Logo

v D = 2513,27 sin ⁡ 40,11 ° sin ⁡ 109,89 ° = 1722 m m s  

Ou no SI

v D = 1,7 m s

E podemos fazer também

v D B = v B sin ⁡ 30 ° sin ⁡ 109,89 °

ω D B = v B r D B sin ⁡ 30 ° sin ⁡ 109,89 °

Isso fica

ω D B = 2513,27 500 sin ⁡ 30 ° sin ⁡ 109,89 ° = 2,67 r a d s

Resposta

ω D B = 2,67 r a d s v D = 1,7 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

71. Se o cilindro hidráulico encurta-se a uma taxa constante de v C = 0,6m / s , determine a velocidade da extremidade A da barra de ligação ACB no instante mostrado.
59. Determine a velocidade angular da engrenagem e a velocidade de seu centro O no instante mostrado.
63. Determine a velocidade do centro de gravidade G da hiela no instante mostrado. O pistao P está se deslocando para cima com uma velocidade de 7,5 m/s.
16.92. Se a extremidade A do cabo é puxada para baixo com uma velocidade V A = 4 m / s , determine a velocidade angular da bobina e a velocidade do ponto C localizado na borda exterior da bobina.
16.94. A roda está rigidamente fixada à engrenagem A , que está engrenada às cremalheiras D e E . Se D tem uma velocidade V D = 1,8m / s para a direita e a roda rola sobre o trilho C sem deslizar, det